Isogonal Kaleidoscopical Polyhedra Families
Vladimir L. Bulatov
Physics Department, Oregon State University, Corvallis, OR
on leave from: Department of Theoretical Physics, St.Petersburg University, St.Petersburg, Russia
Presented at Mosaic2000,
Millennial Open Symposium on the Arts and Interdisciplinary Computing,
21-24 August, 2000,
Seattle, WA
Abstract
A new class of isogonal polyhedra is considered. Polyhedra are constructed using a combination of reflections in several symmetry planes of a given symmetry group. The procedure is a generalization of a Wythoff construction used for building uniform polyhedra. Every valid combination of symmetry planes generates the whole family of isogonal polyhedra. There are seven families with tetrahedral symmetry, 284 with octahedral symmetry and few million with icosahedral symmetry.
1
Introduction
Polyhedra have always been some of the most visually appealing geometrical objects. They have fascinated people from ancient times when the simplest polyhedra - the tetrahedron, cube, octahedron, dodecahedron, and icosahedron ( the platonic solids) were known. Most people's knowledge of polyhedra is usually limited to above mentioned five figures. Twentieth century mathematics has not devoted much attention to polyhedra. Perhaps that is because the subject is very old and too simple from the point of view of modern mathematics. However, polyhedra are extremely interesting objects to investigate and there are many unsolved problems.
One of most most notable polyhedra-related mathematical works of recent times is the paper by Coxeter at all [2], which enumerates all 75 of the so called "uniform" polyhedra. These polyhedra have symmetrically equivalent vertices and regular faces. The requirement of regular faces limits the number of possible figures quite significantly. A much broader set of shapes form polyhedra with symmetrically equivalent vertices - isogonal polyhedra. Actually there are infinite many isogonal polyhedra. Not much is published about isogonal polyhedra: [1] describes so called "noble" polyhedra - polyhedra with equivalent vertices and faces, and [3] gives several interesting new classes of isogonal prismatoids, which are generalizations of prisms and antiprisms. No classification of general isogonal polyhedra has so far been published.
In this paper, we will attempt to describe a subset of all isogonal polyhedra which we call kaleidoscopical polyhedra. These polyhedra may be constructed using the procedure which is similar in some aspects to the process of creating images in a kaleidoscope. We have also attempted computer assisted enumerations of all possible kaleidoscopical polyhedra.
2 Kaleidoscopical polyhedra construction
We will limit our consideration to the following three groups of symmetry: full symmetry of the tetrahedron (Td), octahedron (Oh) and icosahedron (Ih). These are the only point symmetry groups in addition to the simpler dihedral group symmetry of the prism, which consist only of reflections in several symmetry planes and compositions of those reflections. The tetrahedral group Td has six symmetry planes, the octahedral group Oh has nine, and the icosahedral group Ih has fifteen symmetry planes. Isogonal polyhedra should have all vertices equivalent under the operation of a given symmetry group. Therefore all vertices of a polyhedron should lie on a sphere with the center at the origin. The intersection of the symmetry planes with this sphere will be a great circle on this sphere. All such intersections form a grid of great circles. Fig.1a-c show these grids for each symmetry group along with their corresponding platonic solids with that symmetry.
Fig.1 Symmetry planes of selected symmetry groups:
a) Tetrahedral Td
b) Octahedral Oh
c) Icosahedral Ih
Next we choose a "kaleidoscope" - an ordered circular sequence of symmetry planes (i.e. mirrors): [P1, P2, ..., PN]. Let's
call N the order of the isogonal polyhedron. We call the sequence circular, because we assume it to have no beginning and no end, in
that the element following element PN is element P1 again and any circular transposition of a given sequence is considered to be the same sequence. This kaleidoscope resembles the typical real kaleidoscope with the difference that real kaleidoscope has non-penetrating one sided mirrors. Our kaleidoscope has ideal, two sided mirrors possibly penetrating each other.
We can visualize such a kaleidoscope as a spherical polygon on the sphere, whose sides are pieces of great circles.
Fig.2 shows an example of such spherical polygon, which corresponds to kaleidoscope consisting of four mirrors.
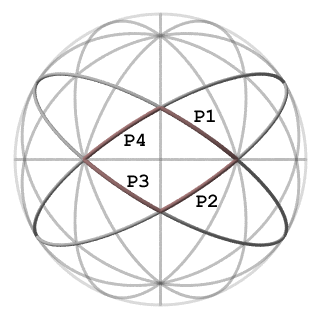
Fig.2 A kaleidoscope is formed by a sequence of symmetry planes.
Sequential mirrors of the kaleidoscope intersects each other along symmetry axis of the symmetry group. The vertices of spherical
polygon are intersections of these symmetry axes with the sphere.
Let's choose an arbitrary point on the sphere (a generator vertex), which will be one of the equivalent vertices of the
kaleidoscopical polyhedron (Fig. 3).
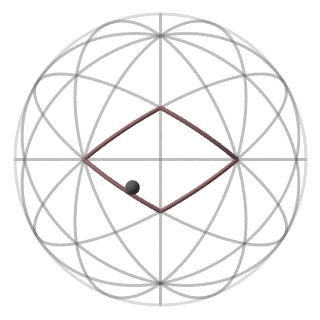
Fig.3 A generator vertex on the sphere.
Every sequential pair of kaleidoscope mirrors is used to form one face of the polyhedron, adjacent to the generator vertex. The vertices of that face are generated from the generator vertex by reflections in symmetry planes. This is the same effect that would happen if we placed a small object representing a vertex inside a wedge formed by two mirrors. We will see the object itself and several of its images. If the dihedral angle between mirrors is rational: (m/n) , then we will have 2*n images. It will not be possible to see all images of the object in the real kaleidoscope because some images will be hidden behind the kaleidoscope wedge, however we will always have all the vertices in our ideal kaleidoscope.
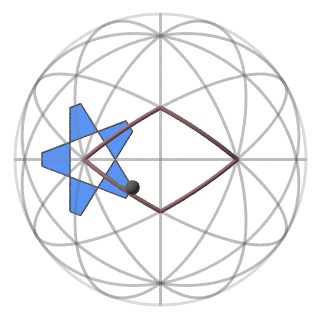
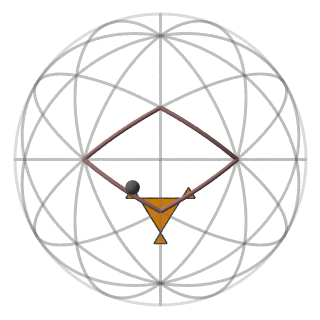
Fig.4a-d shows the faces formed by the generator vertex from each of four pairs of mirrors of our kaleidoscope.
 |
|
|
Fig.4a The face formed by reflections in the symmetry planes P4 and P1. |
Fig.4b The face formed by reflections in the symmetry planes P3 and P4. |
 |
 |
| Fig.4c The face formed by reflections in the symmetry planes P2 and P3. |
Fig.4d The face formed by reflections in the symmetry planes P1 and P2. |
Every sequential pair of faces share a common edge. Each edge joins the generator vertex with its reflection in each mirror common to
both pairs of mirrors used to make each face. Every edge adjacent to the generator vertex has exactly two adjacent faces and we have
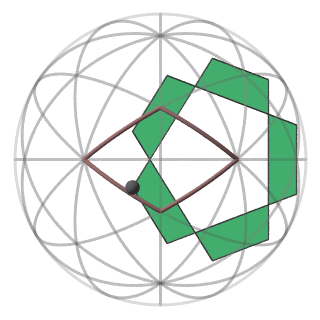
N vertices and N faces adjacent to the generator vertex. Fig.5 shows all four faces adjacent to a generator vertex.
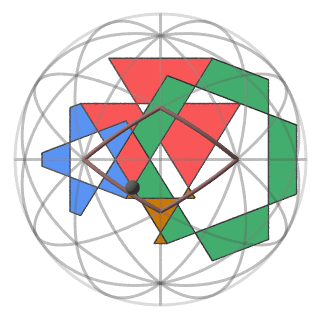
Fig.5 All the faces containing the generator vertex.
The last step in
building the isogonal kaleidoscopical polyhedron is to apply all symmetry transformations of the symmetry group to the faces adjacent to the generator vertex. The beautiful properties of symmetry will cause the resulting shape be a polyhedron with all vertices having N adjacent faces and N adjacent edges. All vertices will be equivalent to the generator vertex.
Fig 6. show such a polyhedron made with a 4-mirrored kaleidoscope.
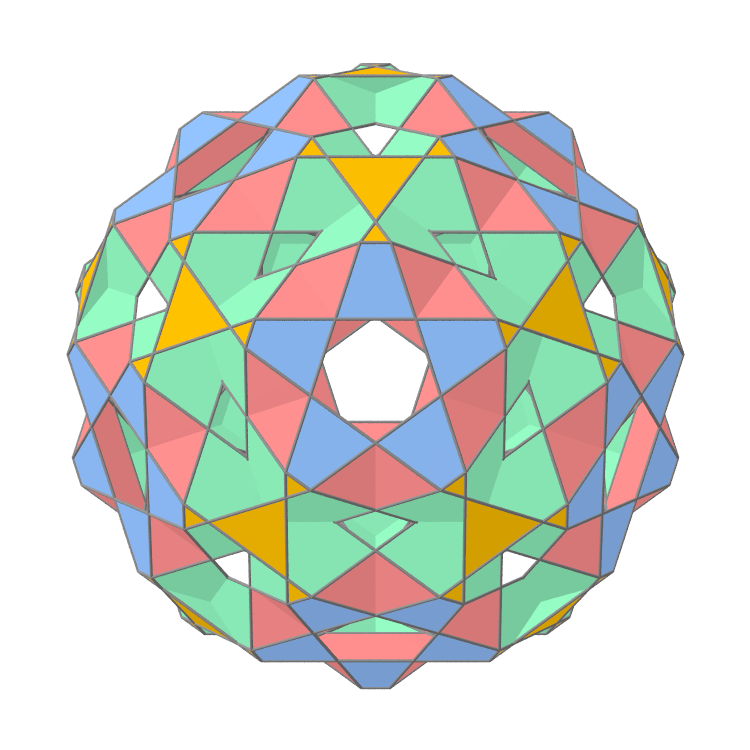
Fig.6 Completed kaleidoscopical polyhedron
(Polyhedron's 5-fold axis is turned to the viewer).
3 Kaleidoscopical polyhedra family
It is important to note that the kaleidoscopical construction described above has one arbitrary parameter - the position of the generator vertex. Every new position of this vertex will create a new polyhedron. All polyhedra constructed using one kaleidoscope and various generator vertex locations will have some common properties. In particular, they will all have the same number of faces, vertices and edges. Moreover, the type of all faces remains the same though the shape of the faces may be very different.
Fig.7 shows the metamorphoses of two different faces types presented in a 4-mirrored kaleidoscope.
Fig.7a Metamorphosis of a kaleidoscopical decagon formed by reflections
in planes P1 and P2.
Fig.7b Metamorphosis of a kaleidoscopical hexagon
formed by reflections in planes P1 and P4.
These drawings are similar to those found in [4].
The metamorphosis of the whole polyhedron is much more complex. Fig.8 attempts to show such a metamorphosis which happens when the
generator vertex moves along a trajectory on the spherical surface.
Fig.8 Metamorphosis of a kaleidoscopical polyhedron.
Fig.8 Metamorphosis of a kaleidoscopical polyhedron (continued).
It is difficult to present in a drawing the real beauty of this polyhedral metamorphosis. It is like trying to show several photos from a real kaleidoscope to give a feeling of operating a real kaleidoscope. Unfortunately it is impossible to make a physical model of this polyhedral transformation, however a computer model can give almost the same effect. We have generated several thousand interactive computer models of kaleidoscopical polyhedra families which can be seen on the web at http://www.bulatov.org/polyhedra/polyhedra/mosaic2000/kaleido_poly/index.html using a standard web browser with a VRML plug-in. These computer models allow interactive real time selection and movement of the generator vertex as well as free rotation of the resulting polyhedron itself.
4
Enumeration of kaleidoscopical polyhedra families
How many kaleidoscopical polyhedra families are there? Not every combination of symmetry planes gives a kaleidoscope which can produce a valid polyhedron. The limitations are:
a) Mirrors may not be coincident. This prevents the creation of polyhedra with coincident edges.
b) The symmetry axes along which sequential mirrors of a kaleidoscope intersect must be unique.
This prevents the creation of polyhedra with coplanar faces.
Not all kaleidoscopes will produce unique families. If there exists a symmetry transformation which maps the mirrors of one kaleidoscope into mirrors of another, the corresponding polyhedral families will be identical. Therefore all equivalent kaleidoscopes can be represented by one arbitrary selected (canonical) representative.
We have conducted a brute force computer search for all possible canonical kaleidoscopes, however the search is not complete. The Table 1 shows the number of families for each symmetry group being investigated. Kaleidoscope with tetrahedral symmetry may have up to 6 mirrors, with octahedral symmetry - up to 9 and with icosahedral symmetry up to 15. Question marks in some cells of icosahedral symmetry mean that the algorithm currently used failed to give results in a reasonable time, however, we think that the nearly one million kaleidoscopes already enumerated give enough material to play with and enjoy. The list of all kaleidoscopical polyhedra is available on the web at
http://www.bulatov.org/polyhedra/mosaic2000/kaleido_poly/index.html
5
Conclusion
We have presented the special class of isogonal polyhedra families which may be constructed using a special kaleidoscopical
construction. The number of such families is quite large, especially for icosahedral symmetry, however the number of arbitrary
isogonal families is significantly larger. Our preliminary attempt to enumerate these families found at least several thousand species
with tetrahedral symmetry Td only seven of which are of the described here kaleidoscopical class.
6
Acknowledgments
I would like to thank Prof. B. Grunbaum for providing information and reprints of his papers on polyhedra. I am also very grateful to
Magnus Wenninger and the Polyhedron mailing list members for numerous inspiring discussions.
References
[1] M.Bruckner. Uber die gleicheckig-gleichflachigen, diskontinuierlichen und nichtkonvexen Polyheder. Nova Acta, Band LXXXVI, #1, Halle 1906]
[2] H.S.M.Coxeter, M.S.Longuet-Higgins and J.C.P.Miller, Uniform Polyhedra. Philos. Trans. Roy. Soc. London, Ser.A v.246, p.401-450, (1954).
[3] B.Grunbaum, Isogonal Prismatoids. Discrete & Computational Geometry. 18, p.13-52(1997).
[4] B.Grunbaum, Metamorphoses of Polygons. The lighter side of Mathematics. Proceedings of the Eugene Strens Memorial Conference on Recreational Mathematics & its History. Edited by Richard K. Guy & Robert E. Woodrow, Mathematical Association of America p.35-48(1994).
Table 1. The count of kaleidoscopical polyhedra families.
|
Symmetry |
| Order |
Ih |
Oh |
Tb |
| 3 |
11 |
7 |
2 |
| 4 |
42 |
9 |
2 |
| 5 |
285 |
26 |
2 |
| 6 |
1579 |
43 |
1 |
| 7 |
9354 |
80 |
aaa |
| 8 |
45471 |
72 |
aaa |
| 9 |
200324 |
47 |
aaa |
| 10 |
622944 |
aaa |
aaa |
| 11 |
? |
aaa |
aaa |
| 12 |
? |
aaa |
aaa |
| 13 |
? |
aaa |
aaa |
| 14 |
? |
aaa |
aaa |
| 15 |
? |
aaa |
aaa |
|
 Vladimir Bulatov abstract creations
Vladimir Bulatov abstract creations