Hyperbolic tiling in a ring
Slides from the talk "Artistic Models of Hyperbolic Geometry"
by
|
|
Use arrows or PgUp/PgDown to navigate slides.
The math equations look best in the Firefox.
Slides from the talk "Artistic Models of Hyperbolic Geometry"
by
|
|
|
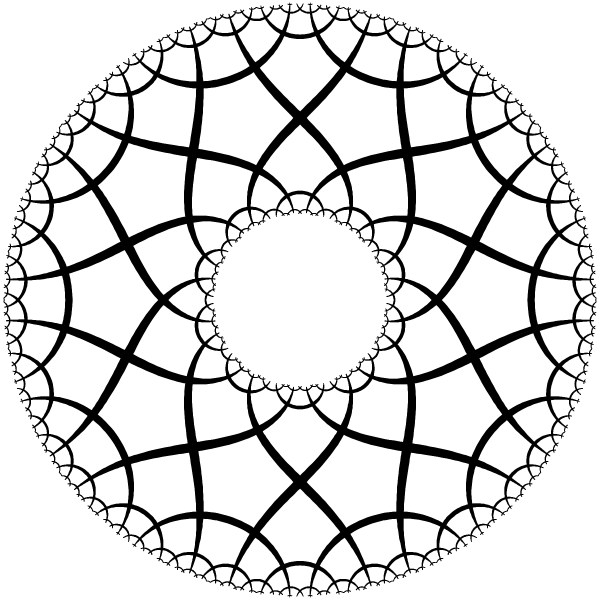
Poincare disk model of hyperbolic plane.
Geodesics in this model are segments of circles orthogonal to the unit circle (circle at infinity).
The model is conformal - the angles between intersecting geodesics are equal to the euclidean angles
between the tangent lines of the circle.
This tiling with right angled regular pentagons is hyperbolic analog of simple square tiling of the euclidean plane. |
|
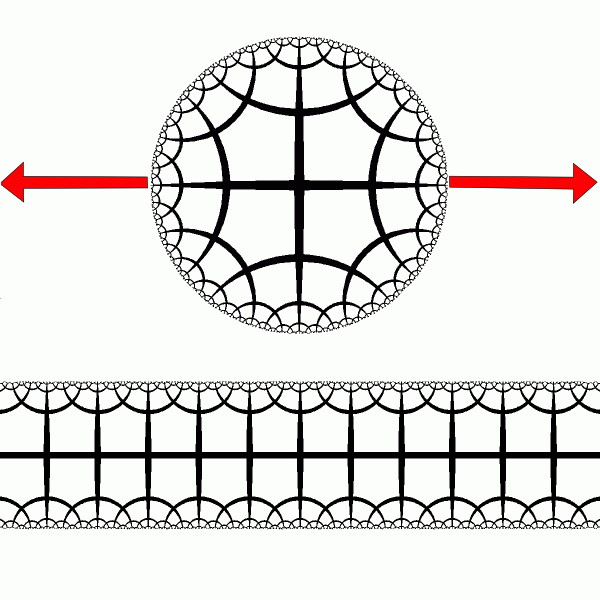
Band model of the hyperbolic plane is obtained by applying to the disk model a special conformal
map of the complex plane:
`w =(4/\pi)tanh\^-1(z);` `z, w \in CC, |Im(w)| < 1, |z| < 1` The band model is conformal, because it is obtained from disk model using conformal transformation. [animation] |
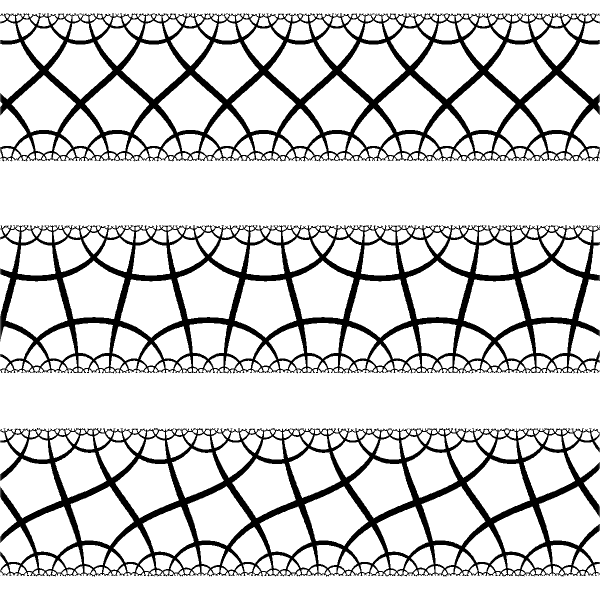
| The same hyperbolic tiling in the band model may have different euclidean periods. The period depends on the particlular location and orientation of the tiling in the disk model before stretching the disk into the band. |
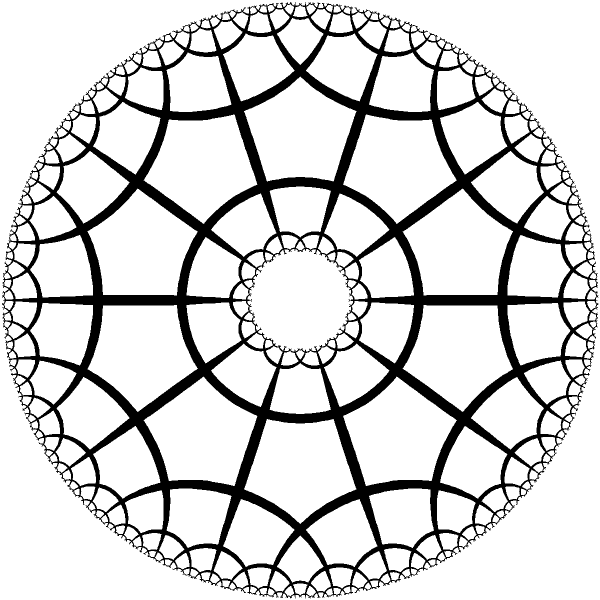
| Ring can be obtained from the infinite band using conformal mapping `w = exp(z/a), z \in CC`. In order to make the tiles match around the ring, the real parameter `a \in R` should be divisible by the euclidean period of the tiling in the band model. There is infinite series of different value such parameters, which makes infinite series of different rings from the same hyperbolic tiling. |
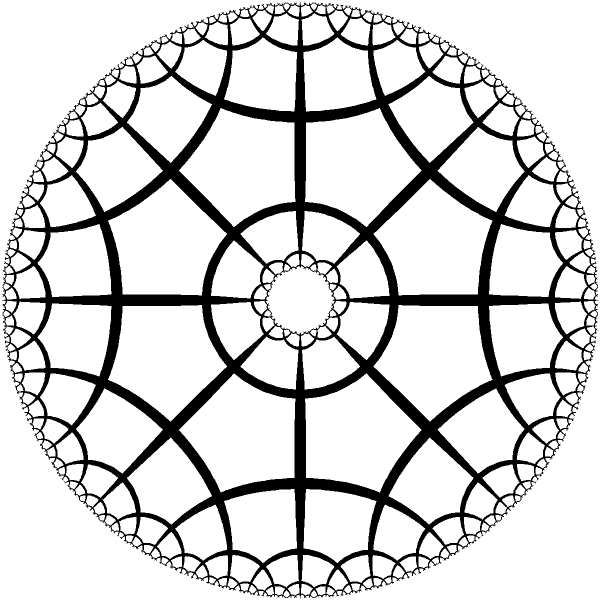
| Ring with 8 periods. |
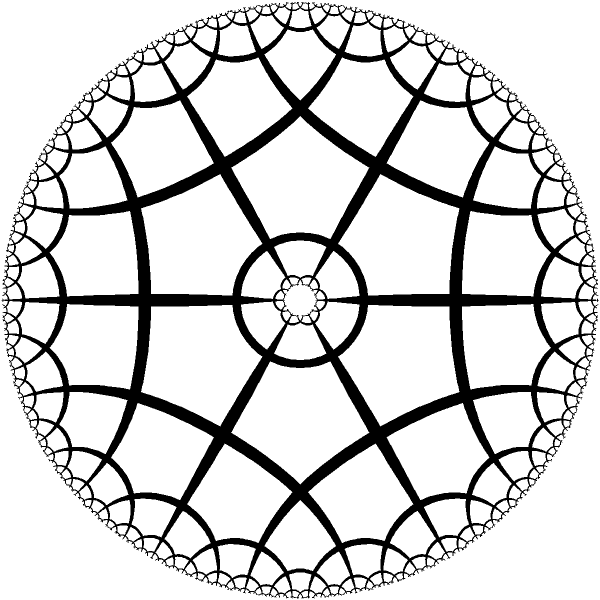
| Ring with 6 periods. |
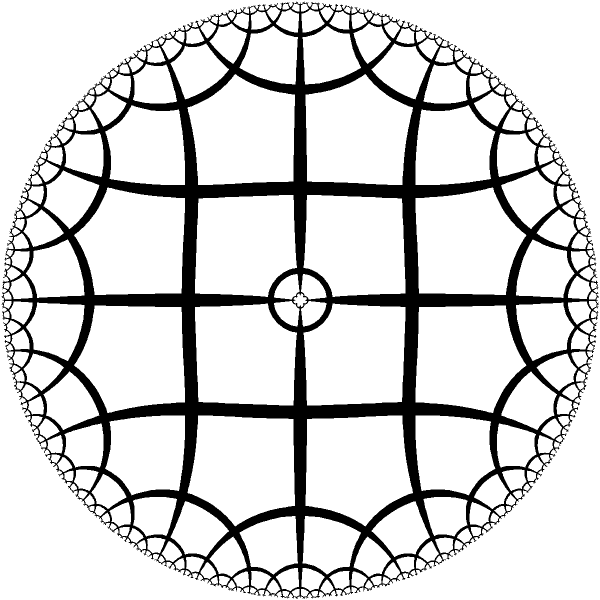
| Ring with 4 periods. |
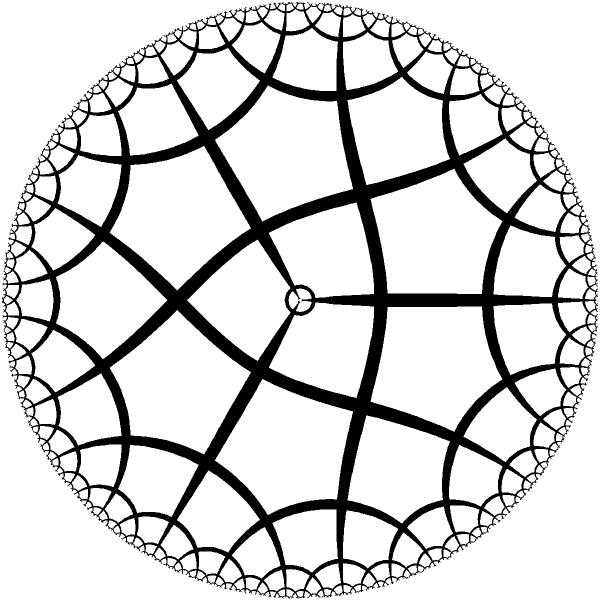
| Ring with 3 periods. |
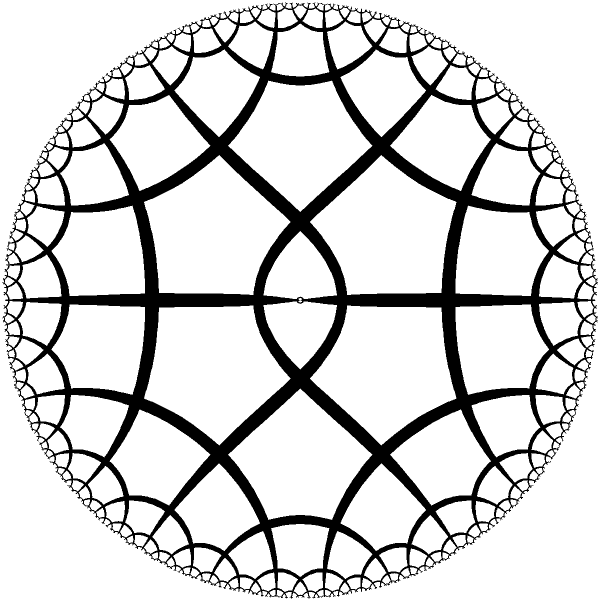
| Ring with 2 periods. |
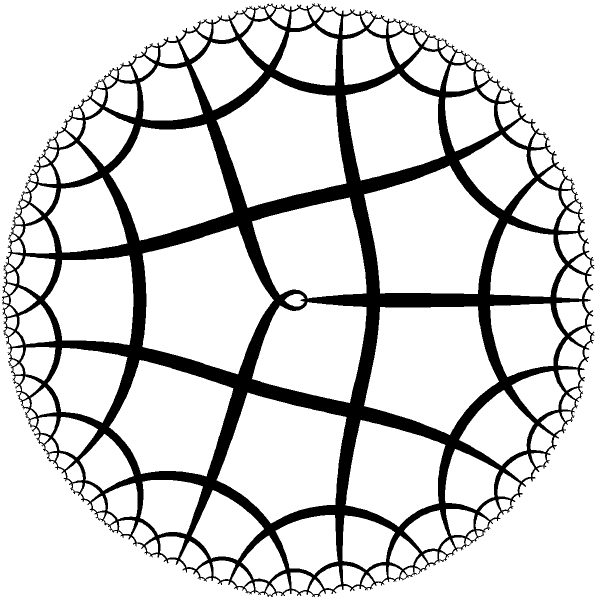
| Smallest ring with only 1 period. The hole in the center is really tiny. |
|
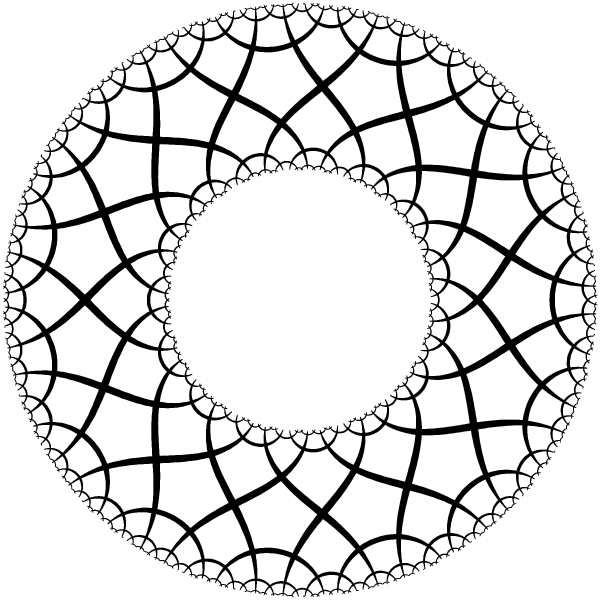
Another infinite series of rings can be generated by different orientation of tiling in the hyperbolic plane.
This is a ring with 15 periods. |
|
| Ring with 10 periods. |
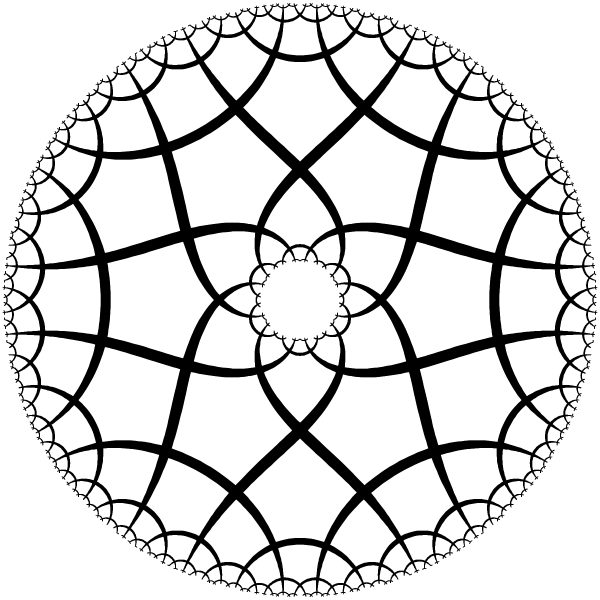
| Ring with 6 periods. |
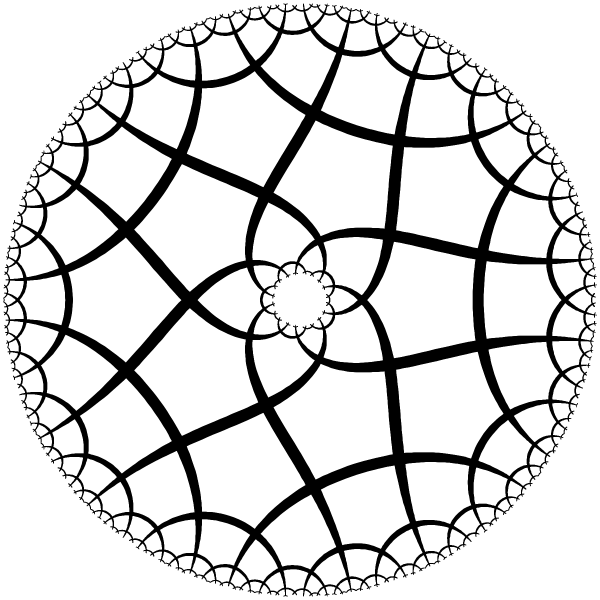
| Ring with 5 periods. |
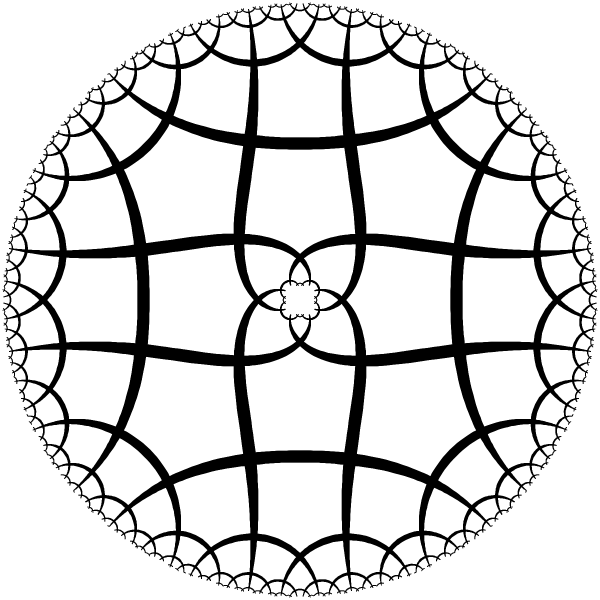
| Ring with 4 periods. |
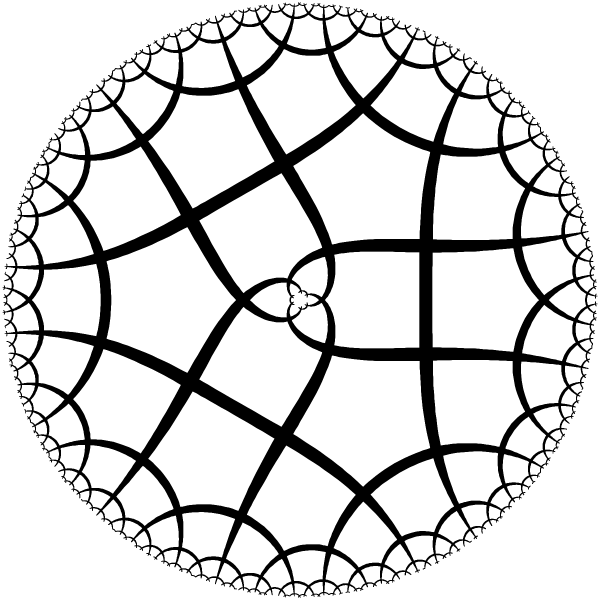
| Ring with 3 periods. |
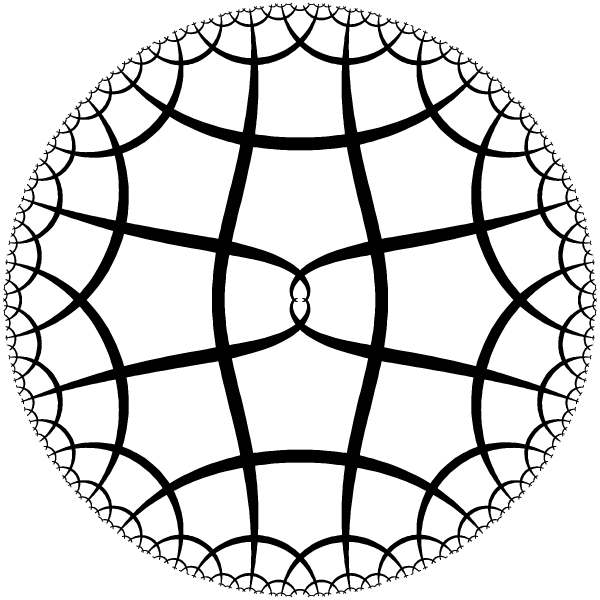
| Ring with 2 periods. |
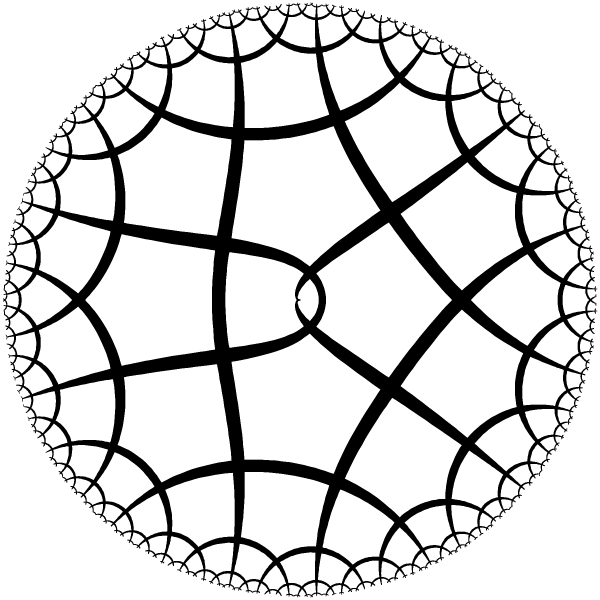
| Ring with 1 period. |
Tiling with 4*3 symmetry. 2 periods.
Tiling with 4*3 symmetry. 3 periods.
Tiling with 4*3 symmetry. 10 periods.
Tiling with 4*3 symmetry. 3 periods.
Tiling with 4*3 symmetry. 10 periods.
Tiling with *832 symmetry. 4 periods.
|
Ring with *24 3 2 symmetry tiling and one period along the ring.
Colored symmetry with 3 colors. |
|
Ring with *642 symmetry tiling and 2 periods along the ring.
Colored symmetry with 2 colors. |
|
Ring with *642 symmetry tiling and 4 periods along the ring.
Colored symmetry with 2 colors. |
|
Ring with *642 symmetry tiling and 6 periods along the ring.
Colored symmetry with 2 colors. |
| Ring with *642 symmetry tiling. 2 periods along the ring. |
| Ring with *642 symmetry tiling. 3 periods along the ring. |
| Ring with *642 symmetry tiling. 4 periods along the ring. |
| Ring with *642 symmetry tiling. 2 periods along the ring. |
| Ring with *642 symmetry tiling. 3 periods along the ring. |
| Ring with *642 symmetry tiling. 4 periods along the ring. |
| Ring with *642 symmetry tiling. 5 periods along the ring. |
|
Ring with *642 symmetry colored tiling. 3 periods along the ring.
3 colors colored symmetry. |
|
Ring with *642 symmetry colored tiling. 6 periods along the ring.
3 colors colored symmetry. |
|
Ring with *642 symmetry colored tiling. 9 periods along the ring.
3 colors colored symmetry. |