Coloring a hyperbolic tiling
Slides from the talk "Artistic Models of Hyperbolic Geometry"
by Vladimir Bulatov
- Perfect Coloring
- Cosets Algorithm
- Coloring of several basic tilings
- Various Examples
|
|
Presented on March 25, 2010 at the Gathering for Gardner 9,
Atlanta, GA.
Use arrows or PgUp/PgDown to navigate slides.
Coloring a hyperbolic tiling
|
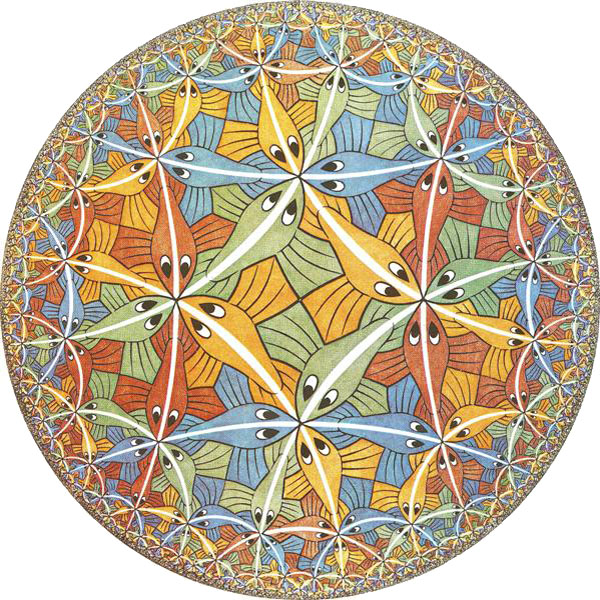
This woodcut "Circle Limit III" by M.C.Escher has identical tiles colored in 4 different colors.
The coloring is "perfect" - individual symmetry transformations change tiles of one colors into tiles of the
same color (this new color may be equal or may differ from the original color).
How can we generate such a perfect coloring?
|
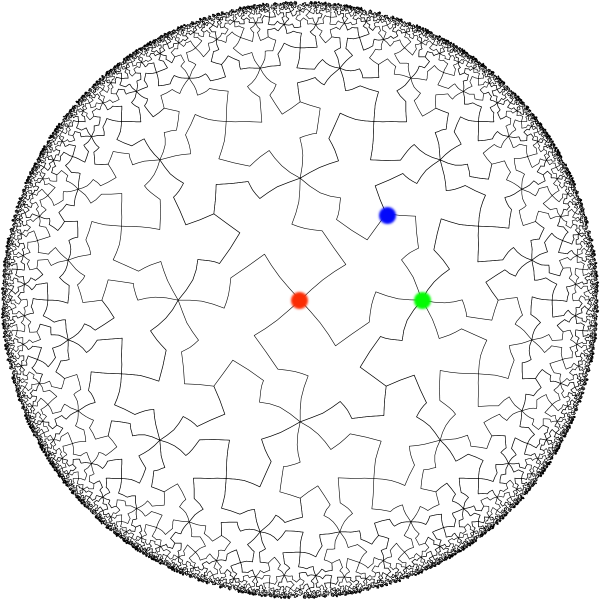
Uncolored tiling
|
Let's start with uncolored tiles. The tiling has hyperbolic symemtry 433. It means, it has one axis of rotations
of 4-th order (marked with red) and two non-equivalent axes of 3-rd order (marked with green and blue).
The set of motions of the hyperbolic plane, which leaves the tilig invariant forms a
group. The groups of symmetry of the
hyperbolic tilings have infinite set of subgroups - a subsets,
which form groups by themselves.
|
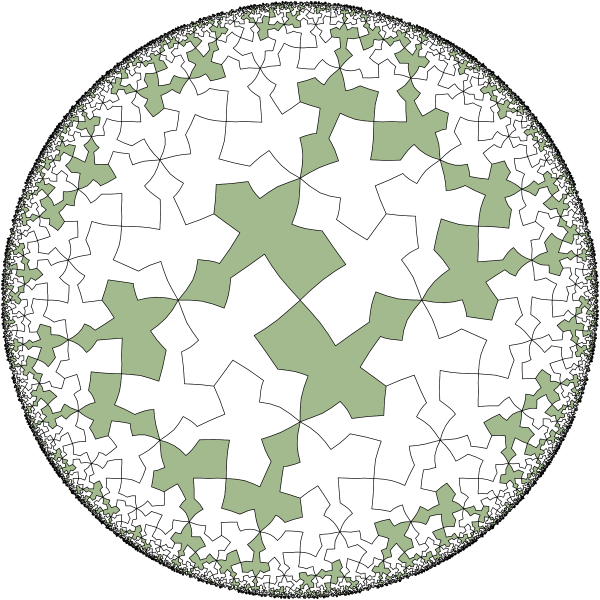
Coloring and subgroups
|
Low index subgroups of a finitely presented grops can be calculated using a computer algebra package
such as GAP.
Let's take a subgroup of index 4 and color in one color all the tiles, obtained from the base
tile by operations from that subgroup.
|
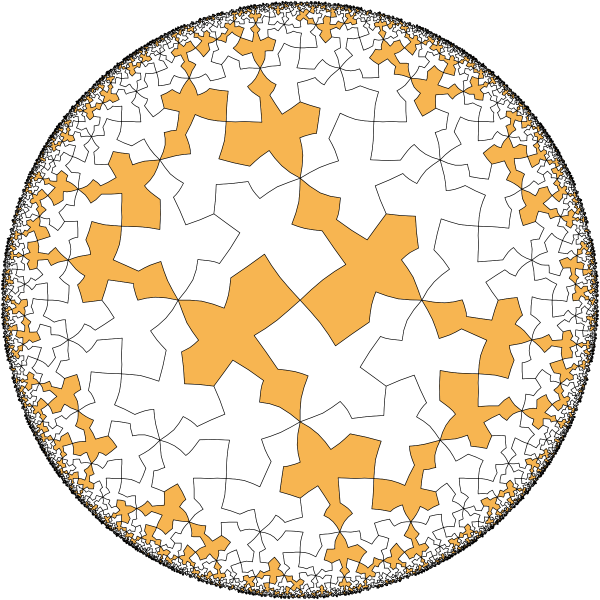
Coloring and subgroups
|
Let's color in different color the tiles obtained from base tile by operations from each coset of that subbgroup.
These are tiles from coset 1.
|
Coloring and subgroups
|
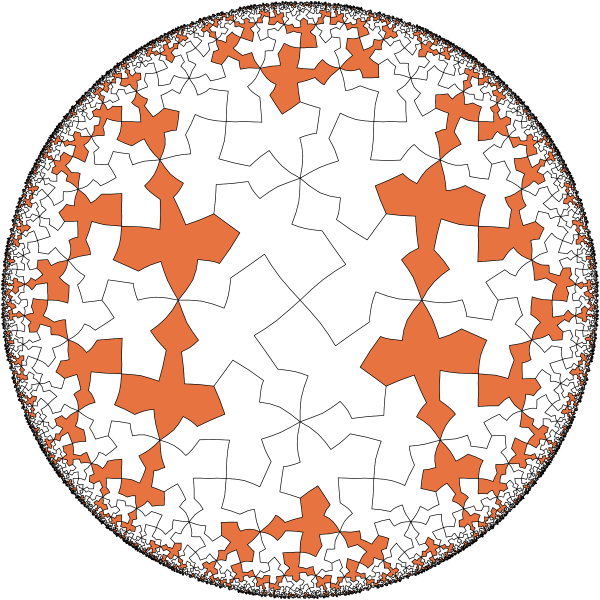
These are tiles from coset 2.
|
Coloring and subgroups
|
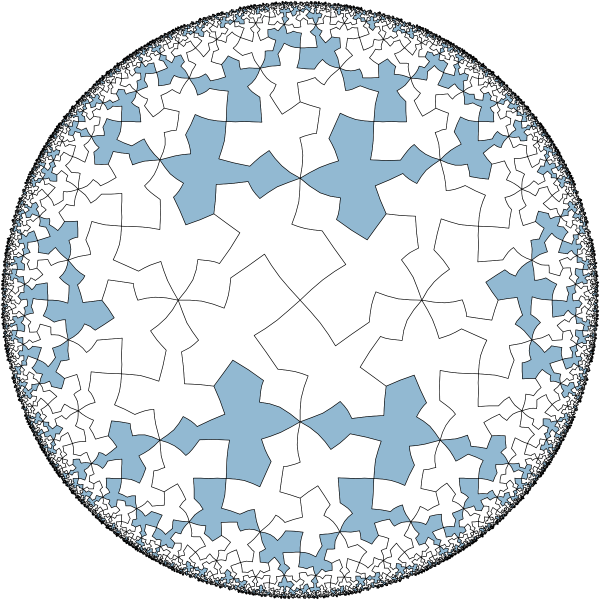
These are tiles from coset 3.
|
Coloring and subgroups
|
Al the colors combined in one image. The coloring is "perfect".
|
M.C.Escher Circle Limit III
|
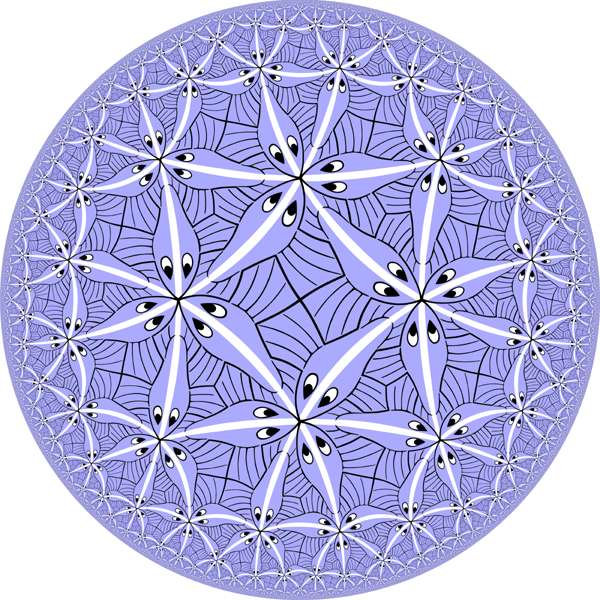
Better rendering of the M.C.Escher "Circle Limit III".
Escher has made it without math and computer. Only compas, straight edge and steady hand. Amazing!
|
M.C.Escher Circle Limit III #2
The same tiling in the band model
M.C.Escher Circle Limit III #3
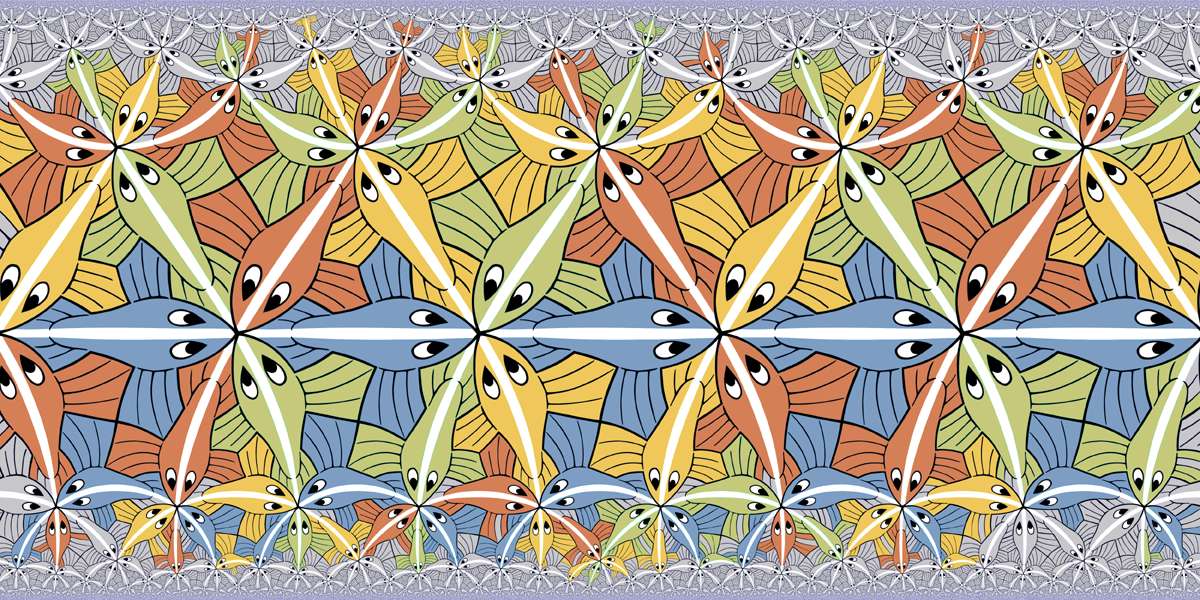
The same tiling colored in 4 colors. Author's software can't render this tiling in color yet.
It was hand colored as far as author pation allowed it.
M.C.Escher Circle Limit III #4
Another orientation of the colored tiling
|
|
Colored tiling *542
The majority of the hyperbolic tilings with colored symmetry were never visualized before.
Here we provide a selection of colored tilings for a few basic hyperbolic symmetries.
Colored triangle tiling with symmetry *542.
The link opens in a new window.
Examples of colored patterns
2 colors. Symmetry 32x.
Examples of colored patterns
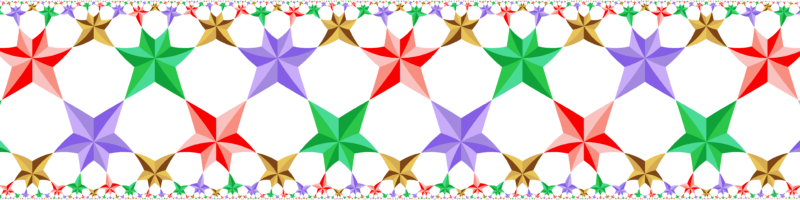
12 colors. Symmetry *642.
Examples of colored patterns
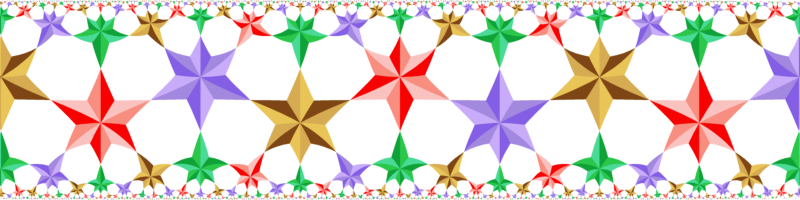
12 colors. Symmetry *642.
Examples of colored patterns
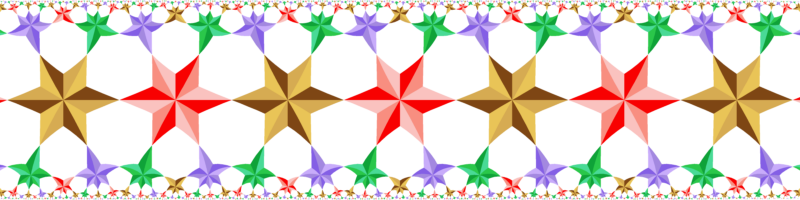
12 colors. Symmetry *642.
Examples of colored patterns
8 colors. Symmetry *642.
Examples of colored patterns
3 colors. Symmetry *642.
Examples of colored patterns
7 colors. Symmetry 642.
Examples of colored patterns
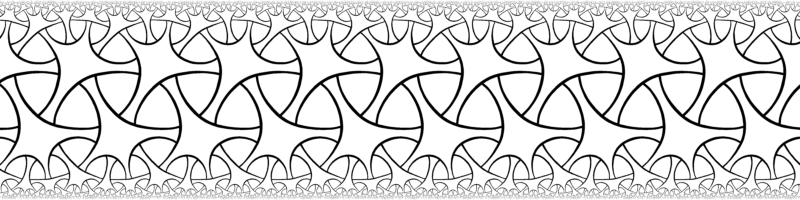
Unclored pattern. Symmetry 433.
Examples of colored patterns
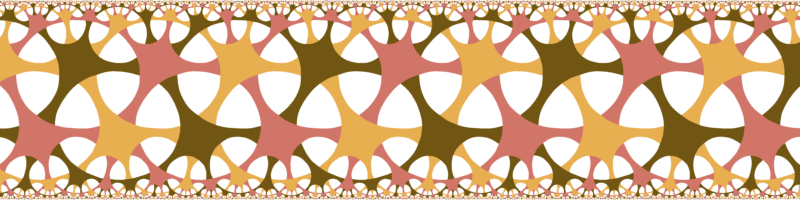
3 colors coloring. Symmetry 433.
Examples of colored patterns
Unclored pattern. Symmetry 3*4.
Examples of colored patterns
3 colors coloring. Symmetry 3*4.
Conclusion
-
Perfect coloring of a hyperbolic tiling can be obtained using "cosets algorithm".
-
There are infinite number of colored symmetries of hyperbolic tilings. Very few of them were classified and visualized before.
Notes on a previous publications
Colored symmetries of the euclidean plane were widely studied from the beginning of 1960s.
However, there are surprisingly few publication on the colored symmetries of the hyperbolic plane.
Only in 2006 and later apears several publications from 2 research groups, which desribe in particular the
"coset algorithm":
De Las Penas M., Felix R., Laigoplane G. , Colorings of hyperbolic plane crystallographic patterns. Z.Kristallogr. 221, (2006) 665-672.
Frettloh D. - Counting perfect colourings of plane regular tilings. Z. Kristallogr. 223 (2008) 773-776
Previous:
Hyperbolic tiling in a ring
Up:
Artistic Models of Hyperbolic Geometry
