Polyhedra Stellation

Introduction

Stellation of polyhedra is a way of creating new polyhedra from existing one via process analogous to creating pentagram from regular pentagon. Every face of polyhedron is extended to infinite plane. These planes divide the 3 dimensional space into number of regions, some of which are infinite some finite. Only finite regions (or elementary cells) are usually considered. In order to obtain symmetrical polyhedron, elementary cells are grouped in symmetrical cells - groups of cells with appropriate symmetry. Any combination of such symmetrical cell is called stellation of original polyhedron.
Usually, to limit number of possible stellation, some restrictions are introduced. For example: only stellations, which form one solid piece, are considered, or only those, which have no exposed inner faces (so called fully supported stellations), etc.
Interactive VRML devices presented here allows construction of stellation with only limitation - symmetry.
Warning: As far as I know on time of this writing, WorldView2.0 from Intervista and CosmoPlayer2.0 from Silicon Graphics are capable to browse these VRML2.0 files.

Instructions

Click on polyhedron name in table below and new window with VRML browser plugin showing corresponding stellation will be loaded. Some default combination of cell will be displayed initially.
Symmetrical cells are represented with set of small red/blue buttons on the right. Red buttons correspond to visible cells. You can switch cells on/off by clicking on corresponding button. Every row of buttons corresponds to one layer of cells. Cells inside of each layer are arranged in order of decreasing volume of cell. The whole polyhedron may be rotated by clicking and dragging it with mouse and may be scaled by dragging red thumb of gray vertical slider.
Warning: There may be some delay caused by transferring data from server after clicking on blue button and before actual appearance of corresponding cell on screen if cell is being displayed first time.

Stellations

Icosahedron, 12 icosahedral cells.
Icosahedron, 42 tetrahedral cells.
Triakistetrahedron (dual to truncated tetrahedron), 11 tetrahedral cells.
Rhombic triacontahedron (dual to icosidodecahedron), 37 icosahedral cells.
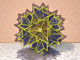Deltoidal (kitoidal?) hexecontahedron (dual to rhombicosidodecahedron) only first 15 layers of total 28, 369 icosahedral cells.
Small stellated truncated dodecahedron , 21 icosahedral cells.

e-mail: vladimir@bulatov.org