
{6,4} - simple cubic lattice formed by truncated octahedra with holes instead of squre faces. Four hexagons meet at every vertex.

{6,4} - simple cubic lattice formed by
truncated octahedra with holes instead of squre faces. Four hexagons
meet at every vertex.
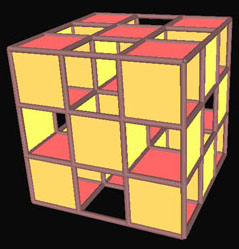
{4,6} - lattice of cubes with
some faces removed. Six squares meet at every vertex.

{5,5} - lattice of regular
pentagons, 5 at each vertex.
{3,8},
{3,12},
another {3,12}
These polyhedra models are from Melinda Green's geometry page.
© Copyright 1997 V.Bulatov. Commercial use of these materials is prohibited without prior written permission.
 e-mail:
vladimir@bulatov.org
e-mail:
vladimir@bulatov.org