 Vladimir Bulatov abstract creations
Vladimir Bulatov abstract creations
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
 |
 |
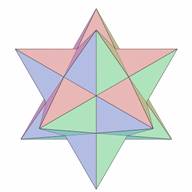
| Figure 1. Small Stellated Dodecahedrom |
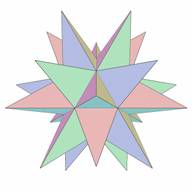
Figure 2. Great Stellated Dodecahedron |
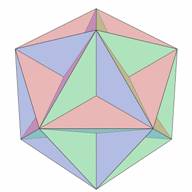
Figure 3. Great Dodecahedron |
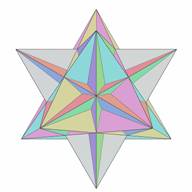
Figure 4. Great Icosahedrom |
Polyhedra Stellation
Polyhedra stellation is a way of creating a new polyhedron from an existing one via a process similar to creating a pentagram from a regular pentagon. In the case of a pentagon every side of the pentagon is extended in both directions beyond the pentagon's vertices. These extended lines will break the plane into 16 areas: the original pentagon, 5 triangles and 10 infinite areas. The pentagon's stellation then is any combination of the 6 finite areas. Often, however, only the most symmetric combination of these shapes, namely the pentagram, is called a stellation.
Similarly, one can extend the faces of a polyhedron in all directions. The set of these infinite planes will divide the three dimensional space into a number of convex regions, some finite and some infinite. Only finite regions (elementary cells) are used as building blocks for stellations. We define a polyhedron stellation as any combination of elementary cells. The polyhedron, which was stellated, is called also the core polyhedron . Our definition of stellation is very loose compare to other definitions, which are often used. The most important difference is that our definition allows arbitrary symmetry of stellation, which allows a wider than usual variety of polyhedral shapes.
Usually the core polyhedron has some symmetry. This means that there is a set of geometrical transformations, which transforms the polyhedron into itself. The complete set of these transformations forms a symmetry group of the core polyhedron. The set of transformations is a group in the mathematical sense, because the product of any two transformations is again a transformation, which leaves the polyhedron invariant. Therefore it should belong to the set. For more detailed discussion of polyhedral symmetry see [1]. The number of transformations in the symmetry groups is called the order of the group. The symmetry of the core polyhedron allows the division of all elementary stellation cells into an array of equivalent elementary cells. We call such an array of symmetrically equivalent elementary cells a complete stellation cell . From group theoretical point of view complete stellation cell is the orbit of an elementary cell under the action of the symmetry group.
The icosahedron and dodecahedron have diploid icosahedral group Ih (order 120), the octahedron and cube have diploid octahedral symmetry group Oh (order 48), the tetrahedron has diploid tetrahedral symmetry group Td (order 24).
The number of elementary cells in a complete stellation cell may vary, but it should always be a divisor of the group's order. For example the polyhedron of symmetry Ih may have complete cells of size 120, 60, 30, 20, 12, 1 (core polyhedron).
The complete stellation cell always has the same symmetry as the core polyhedron. Therefore any combination of complete stellation cells will have the same symmetry as the core polyhedron. In order to introduce more variety into the possible symmetry of stellation we will use arrays of elementary cells with lower symmetry than the symmetry of the core polyhedron. The natural choice for such lower symmetry is any subgroup H of the original symmetry group G. A subgroup of any symmetry group is a subset of geometrical transformations of the symmetry group, which itself is a group. For example, diploid icosahedral group Ih has subgroup C5 (5-gonal group of order 5), which consists of five rotations 2 π n/5 ( n = 0,1,2,3,4) about one of the icosahedron's axes of 5th order. We call a stellation subcell of symmetry H an array of elementary stellation cells which is invariant under operations of subgroup H.
The complete stellation cells are arranged into layers, that is, a set of cells which covers all previous layers. A more formal definition of a layer number is this: it is the number of stellation planes which will be crossed by a ray from the center of a polyhedron core to some point inside of any elementary cell. Layer number 0 is the core polyhedron itself. The lowest layers of some polyhedra stellations often have only one complete cell. A few upper layers often have holes.
Every elementary stellation cell has two kinds of facets: top and bottom facets. The top facets are parts of planes which are located above the cell relative to the polyhedron's center. The bottom facets are parts of polyhedron planes located below the cell. We say that a cell is supported if it has adjacent cells for every one of its bottom facets. Core polyhedron is the only cell which has no bottom facets and it is automatically "supported". Important kinds of stellations are the fully supported stellations. These are stellations with all cells supported. These stellations look more like traditional polyhedra - solid shapes without voids.
Stellation example: Icosahedron stellation
We will illustrate the general ideas of stellation described above with some examples of the stellation of an icosahedron. The choice of this relatively simple icosahedron stellation is to make more clear the symmetry approach introduced in the paper.
For the purpose of model building one needs to have a plot of all faces of the model. It is obvious, that all faces lie in the planes of the core
polyhedron. Intersections of the extensions of any selected polyhedron face with all other face planes are infinite lines, which lie in the selected
plane. We will eliminate the infinite segments of these lines, which form infinite faces of infinite elementary cells. The remaining finite segments
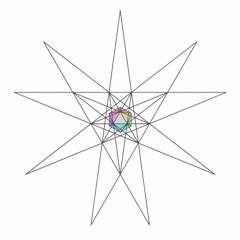
form the so called stellation diagram. Fig.5 shows the stellation diagram of the icosahedron with its center core icosahedron attached to it.
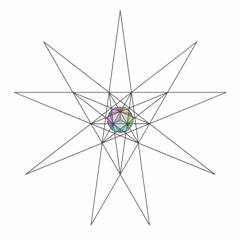
The icosahedron has only one stellation diagram because all its faces are equivalent. Fig.6 shows the complete stellation cell of the first
layer 1(0) with the stellation diagram attached to it. This complete cell consists of an array of 20 elementary cells - triangular pyramids attached
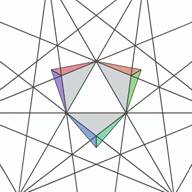
to every face of the core. Figs. 7 and 8 show three of these elementary cells.
 |
 |
| Figure 5. Icosahedron stellation. Icosahedron (cell 0(0)) with attached face diagram) |
Figure 6. First stellation of icosahedron (cell 1(0)) with attached face diagram) |
 |
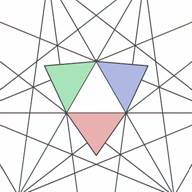 |
| Figure 7. Three elementary cells of layer #1 (top view) | Figure 8. Three elementary cells of layer #1 (bottom view) |
One facet of each of these elementary cells lies in the plane of the stellation diagram. Two other identical facets occupy similar places in the stellation diagrams attached to other icosahedron faces. The bottom of each pyramid is a face of the core icosahedron, which in turn has equivalent faces in the center of the diagram.
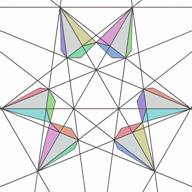
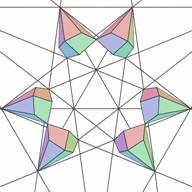
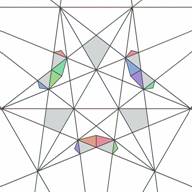
Not all layers of the icosahedron's stellation are formed by cells of one kind. Layer 4 has 20 elementary cells of one type (let's say type 0) , (Figs. 9 and 10) and 60 elementary cells another type (let's say type 1) (Figs.11 and 12).
 |
 |
 |
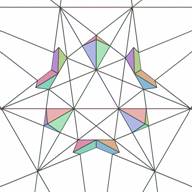 |
| Figure 9. Six elementary cells of stellation cell 4(0)- layer #4, type 0 (top view) | Figure 10. Six elementary cells of stellation cell 4(0) (bottom view) | Figure 11. Nine elementary cells of stellation cell 4(1) - layer #4, type 1 (top view) | Figure 12. Nine elementary cells of stellation cell 4(1) (bottom view) |
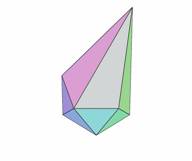
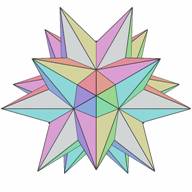
Now we will look at one elementary cell from layer 4 of type 0 (Fig.13). The fully supported stellation for this cell is shown in Fig.14. It is clear from this figure which icosahedral planes were used to form the facets of the elementary cell. The complete stellation cell, formed by an array of elementary cells is shown in Fig.15 (stellation e1 from [2]). The fully supported stellation for this cell is shown in Fig.16 (stellation De from [2]).
 |
 |
 |
 |
| Figure 13. Icosahedron and one elementary cells of stellation cell 4(0) from Figure 5 |
Figure 14. Fully supported stellation for elementary cell from the left |
Figure 15. Stellation cell 4(0) consists 20 elementary cell shown at Figure 9 |
Figure 16. Fully supported stellation S{4(0)} |
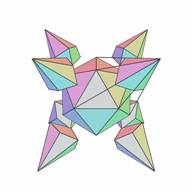
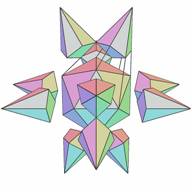
Now we will choose a symmetry of stellation which is the central tetrahedral symmetry Th - the symmetry of a cube inscribed in the icosahedron. This causes a split in the 20 elementary cells array into two subcells consisting of 8 and 12 elementary cells (Figs. 17 and 19). Figs. 18 and 20 show the fully supported stellations for these subcells. It is noteworthy to mention that it is easy to mistake the symmetry of the subcell of Fig. 17 for the octahedral symmetry Oh, but is really only symmetry Th, because it has no axes of 4th order.
 |
 |
 |
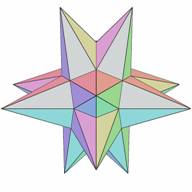 |
| Figure 17. Subcell Th:4(0[0]) | Figure 18. Fully supported stellation S{Th:4(0[0]) } |
Figure 19. Subcell Th:4(0[1]) | Figure 20. Fully supported stellation S{Th:4(0[1])} |
Use of the stellations applet
The stellations applet [11] was written to greatly facilitate the process of stellation construction. The main purpose of the applet is to help the user find and select interesting stellations and to provide face diagrams showing patterns useful for making models. The applet will run on any computer system, which has java runtime environment. It also runs inside of standard web browsers.
There are two different user interface widgets, which allow the selection of a stellation. One way is to use a list of all stellation cells. They are grouped into layers, cells and subcells (Fig. 25). Cells and subcells are color coded to show how many elementary cells they contain. The user can turn on/off any cell, subcell or the whole layer by a mouse click on the corresponding box. A very useful feature is to turn on/off all the cells or subcells, which form a fully supported stellation with a given cell on the top. For example, the stellation shown in Fig. 26 was created by one mouse click on the topmost cell, which causes the inclusion of 73 subcells into the stellation. One can see myriads of these cells in Fig. 26. All together they make a simple and attractive model, which looks like a twisted version of the small stellated dodecahedron.
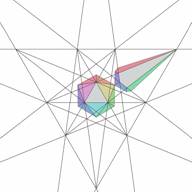
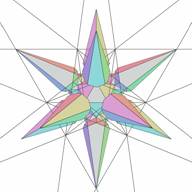
Another way of selecting stellation cells is to pick up the cell directly from the stellation diagram. This is a process less obvious for the user. The first difficulty is that most of the facets on a stellation diagram have two cells attached to them - from the top and from the bottom. Examples are given in Figs. 21 and 22, Figs. 23 and 24, showing the corresponding complete cells.
 |
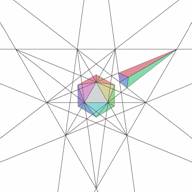 |
| Figure 21. Core icosahedron and elementary bottom cell for selected facet | Figure 22. Core icosahedron and elementary top cell for selected facet |
 |
|
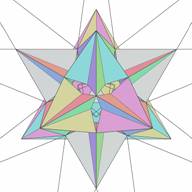
| Figure 23. Core icosahedron and complete bottom cell for selected facet | Figure 24. Core icosahedron and complete top cells for selected facet. It is clear, that this complete cell is simultaneously a bottom cell for other facets of the stellation plane. |
Facets with top attached cells are colored red, with bottom attached cells are colored yellow. Another difficulty is the complexity of relationship of stellation facets. An inclusion of a new facet may require addition or removal of a whole bunch of other facets, which may often not be obvious, but which is done automatically by the computer.
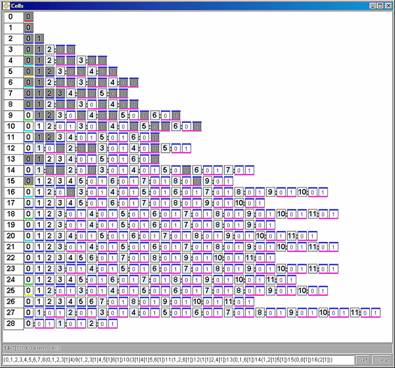 |
Figure 25. Cells of a supported stellation S{I:16(2[1])} of strombic hexecontahedron (dual to rhombicosidodecahedron). Selected cells are marked with gray. It consists of 73 stellation cells and few hundreds elementary cells, but may be easy generated using one mouse click in the stellation applet |
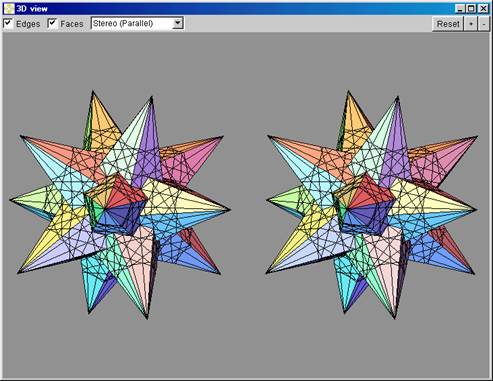 |
Figure 26. Stereo display of the stellation above |
Conclusion
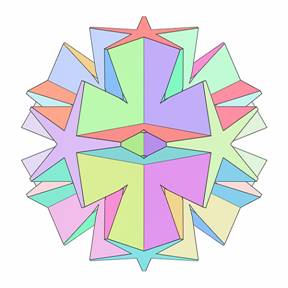
The Polyhedra Stellations Applet is a very powerful tool for constructing new polyhedra. The use of different stellation symmeties helps to create new and beautiful shapes, using old familiar solids. We consider the Polyhedra Stellations Applet to be very useful because of the aesthetic quality of the shapes it allows the user to generate. As an example, Fig.27-30 represent a several fully symmetrical stellation of various polyhedra and . 31 gives some fully supported stellations of the icosahedron with diploid skew 5-gonal symmetry D5d. The creation of new stellation shapes never was so easy.
 |
 |
||
| Figure 27. Stellation of strombic hexecontahedron | Figure 28. Stellation of strombic hexecontahedron | ||
 |
 |
||
| Figure 29. Stellation of small retrosnub icosicosidodecahedron | Figure 30. Stellation of triakisicosahedron | ||
 |
|||
| Figure 31. A set of icosahedron's stellations with stellation's symmetry D5d | |||
Acknowledgements
I am very grateful to Norman Johnson, George Olshevsky, George Hart, Vincent Matsko and Peter Messer for help and numerous fruitful discussions and especially to Magnus Wenninger for his valuable help and advise.
References
[1] Peter R.Cromwell, Polyhedra. Cambridge University Press, 1997.
[2] H.S.M. Coxeter, P. DuVal, H.T. Flather, and J.F. Petrie, The Fifty-Nine Icosahedra, U. Toronto Pr.,
1938, (Springer-Verlag reprint, 1982), (Tarquin reprint 1999).
[3] Alan Holden "Shapes, Space, and Symmetry" (p. 90) Dover, 1971
[4] George Olshevsky "36 dodecahedra". 1996, private communication.
[5] George Hart. Tetrahedral Stellations of the Icosahedron, Tetrahedral Stellations of the Dodecahedron,
1996 http://www.georgehart.com/virtual-polyhedra/stellations-icosahedron-tetrahedral.html
http://www.georgehart.com/virtual-polyhedra/stellations-dodecahedron-tetrahedral.html
[6] Vincent J. Matsko "Some irregular Pentagonal Dodecahedra", 1997. Private communication.
[7] Vladimir Bulatov. 270 Dodecahedra, 1997.
http://www.bulatov.org/polyhedra/dodeca270/index.html
[8] Vladimir Bulatov. Polyhedra Stellations. 1998
http://www.bulatov.org/polyhedra/stellation/index.html
[9] Magnus J. Wenninger. Polyhedron Models. Cambridge University Press. 1971
[10] Magnus J. Wenninger. Dual Models. Cambridge University Press. 1983.
[11] Vladimir Bulatov. Stellations Applet. 2000.
http://www.bulatov.org/polyhedra/stellation_applet/index.html
[12] Hugo F. Verheyen Symmetry Orbits. Birkhauser, 1996
[13] Peter W. Messer. Stellations of the rhombic triacontahedron and beyond.
Structural Topology 21, pp 25-46, 1995.