3D Hyperbolic Tiling and Horosphere Cross Section
Vladimir Bulatov,
Shapeways
Joint AMS/MAA meeting
San Diego, January 10, 2018

Vladimir Bulatov,
Shapeways
Joint AMS/MAA meeting
San Diego, January 10, 2018

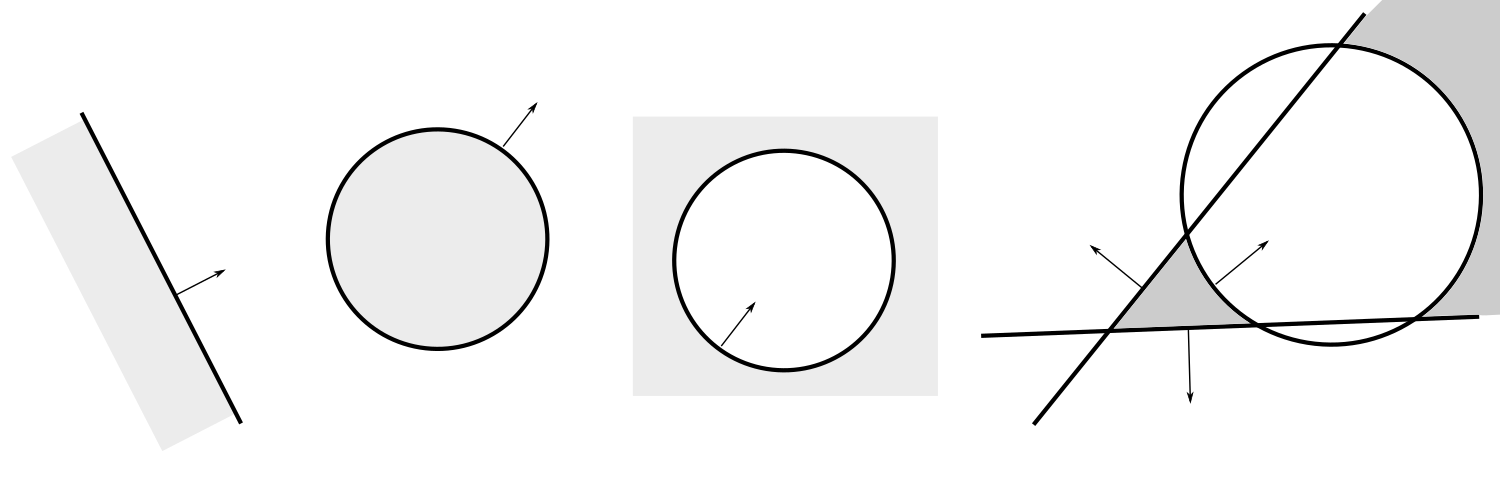
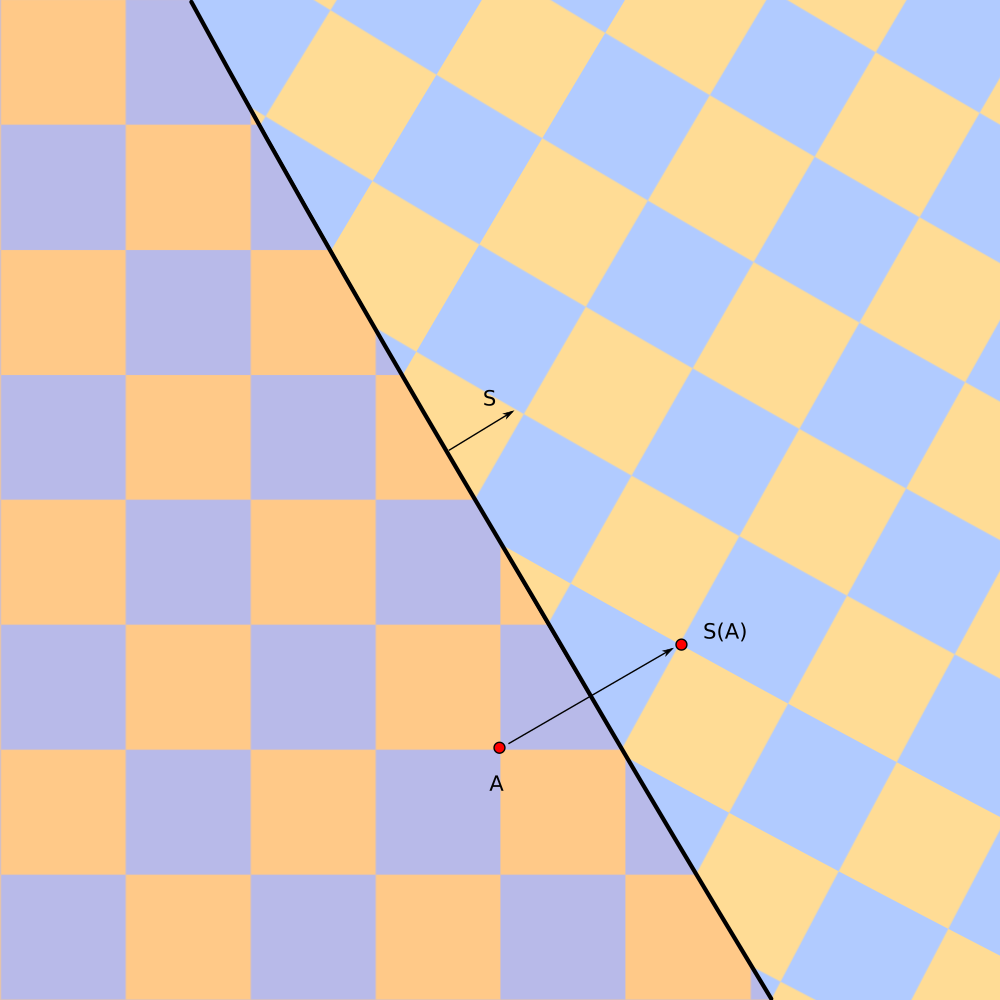
Region on the right looks like two components region, however it is an infinite cheese wedge with a spherical hole.
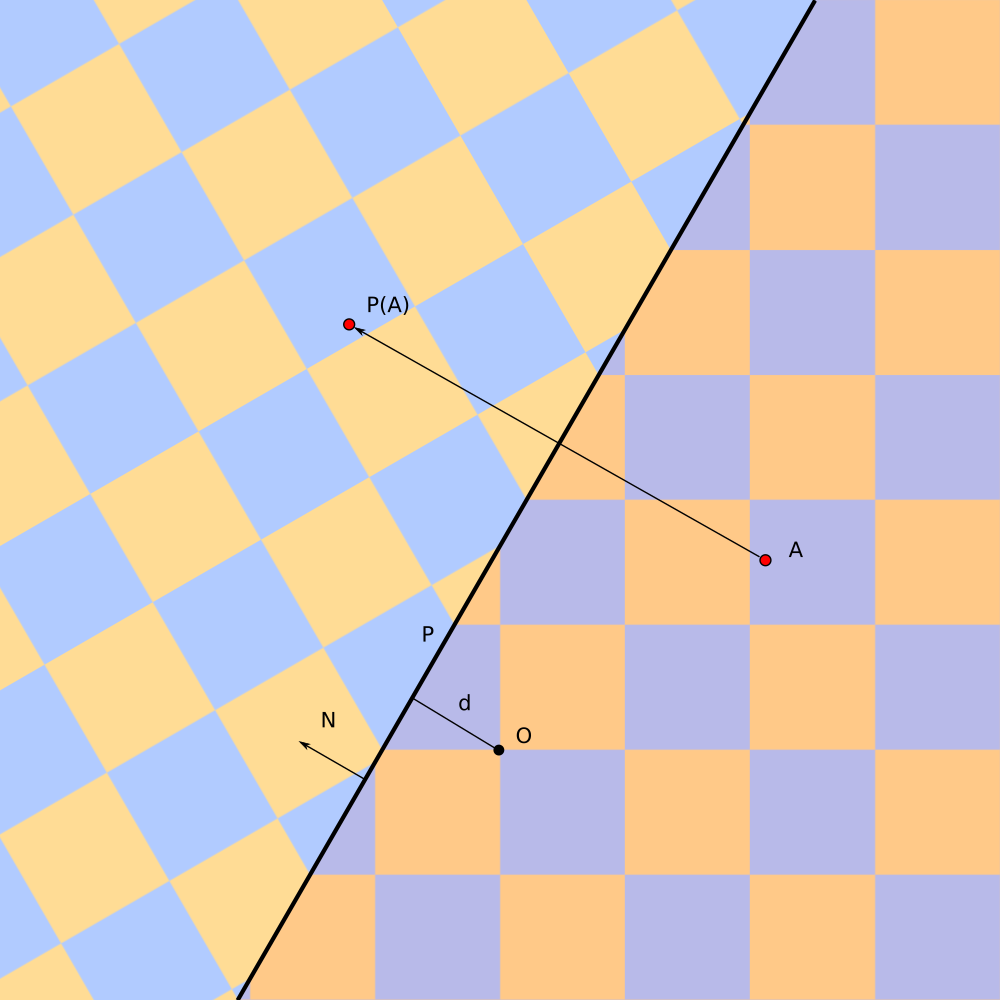
Plane `P {N, d}` is defined via `N` - vector of external normal and `d` - distance of plane to origin `O`.
Reflection in plane `P` maps point `A` into point `P(A)`
`P(A) = A - 2 << A - d N, N >> N`.
Where `<< , >>` is scalar product.
Signed distance of point `A` to to plane `P` is
`P(S, A) = << A, N >> - d`
Here we have mapped interior region of the plane (on the right) on the exterior region on the left.
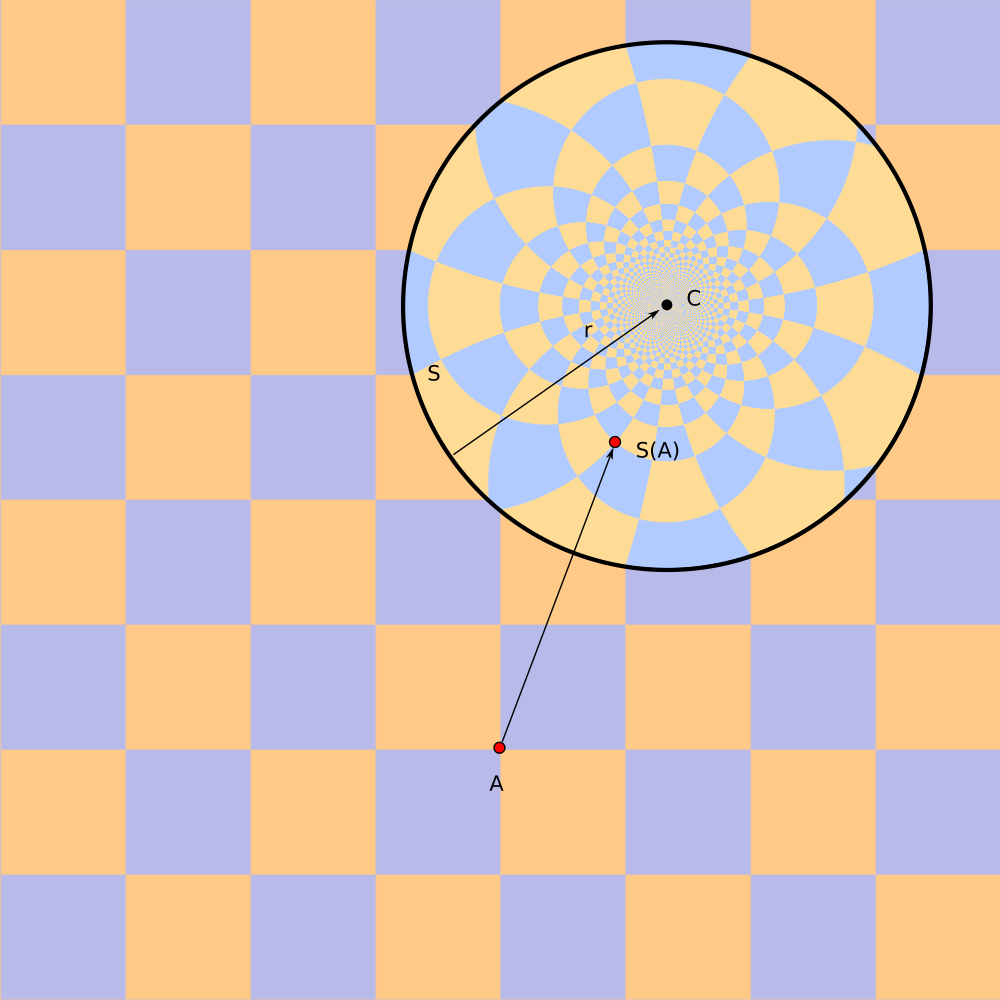
Sphere `S{C,r}` is defined via center `C` and signed radius `r`.
Positive radius means interior of splane `S` is region inside of the ball.
Negative radius means interior of splane is region outside of the ball.
Inversion in sphere `S` maps point `A` into point `S(A)`
`S(A) = C + r^2/|A - C|^2 (A-C)`
Signed distance of point `A` to to sphere `S` is
`D(S, A) = sign(r) (|A-C| - |r|)`
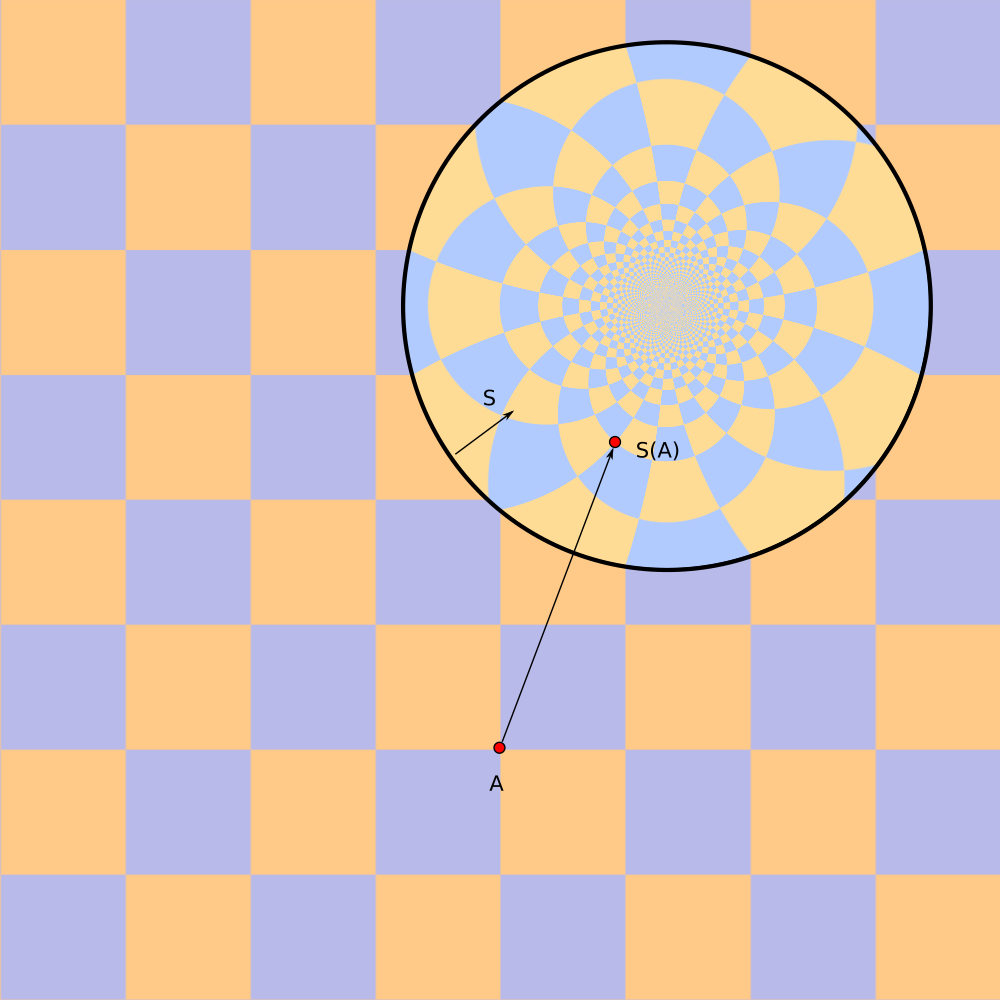
Inversion is sphere becomes reflection in plane when radius of sphere tends to infinity.

Inversion is sphere becomes reflection in plane when radius of sphere tends to infinity.

Inversion is sphere becomes reflection in plane when radius of sphere tends to infinity.
Inversion is sphere becomes reflection in plane when radius of sphere tends to infinity.

Tiling can be constructed in several steps

Tiling can be constructed in several steps

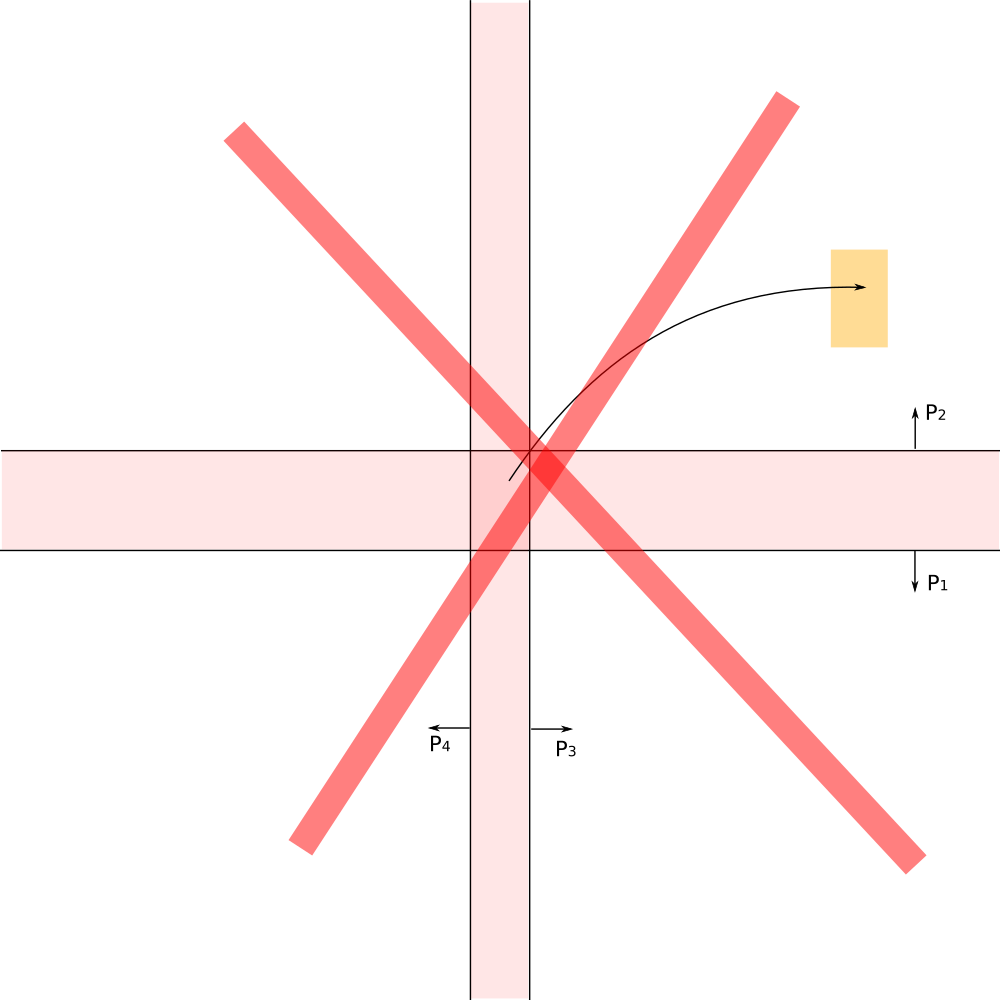
Straightforward appoach - apply each of transformation of the group to the fundamental domain.
Troubles
Straightforward appoach - apply each of transformation of the group to the fundamental domain.
Troubles
Different apporach is needed!

Different approach - draw only pixels which we can see.
For each visible pixel on the screen find transformation which maps it to the corresponding pixel in the fundamental domain.
Color the pixel with color of the corresponding pixel in the fundamentral domain.

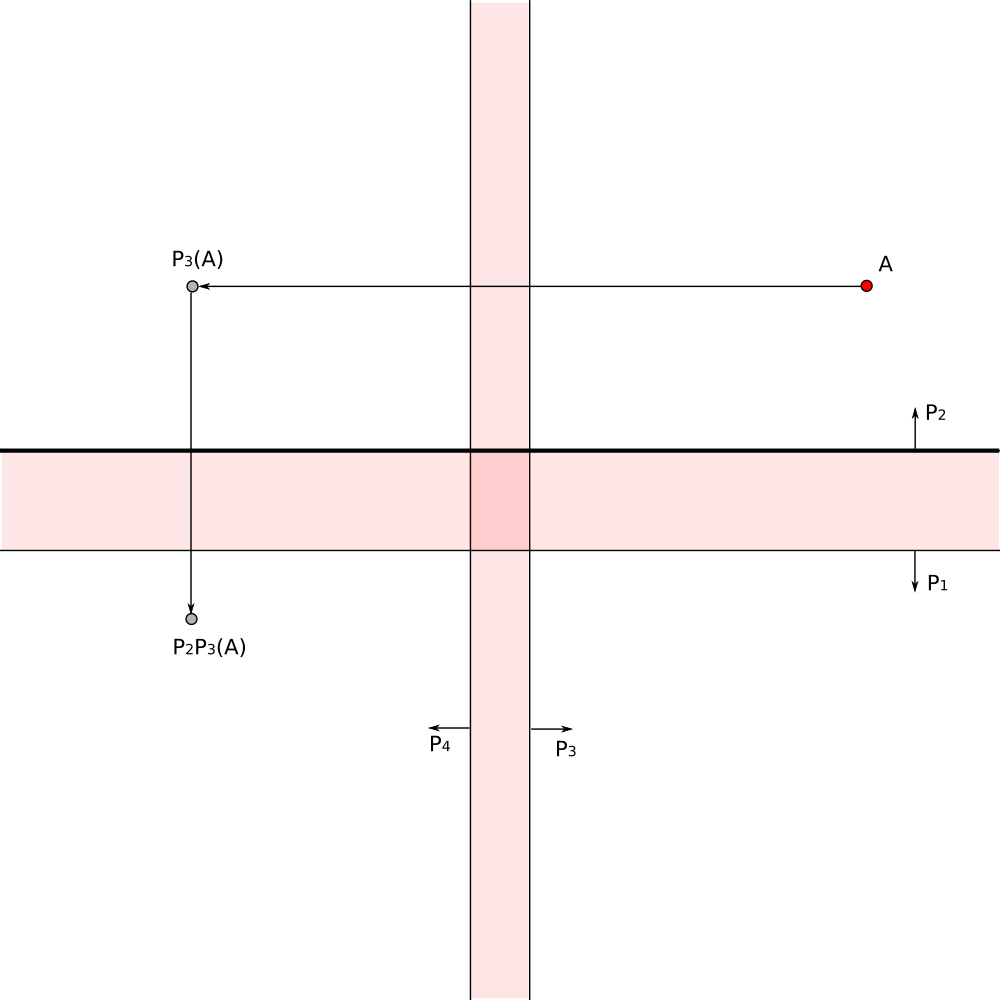
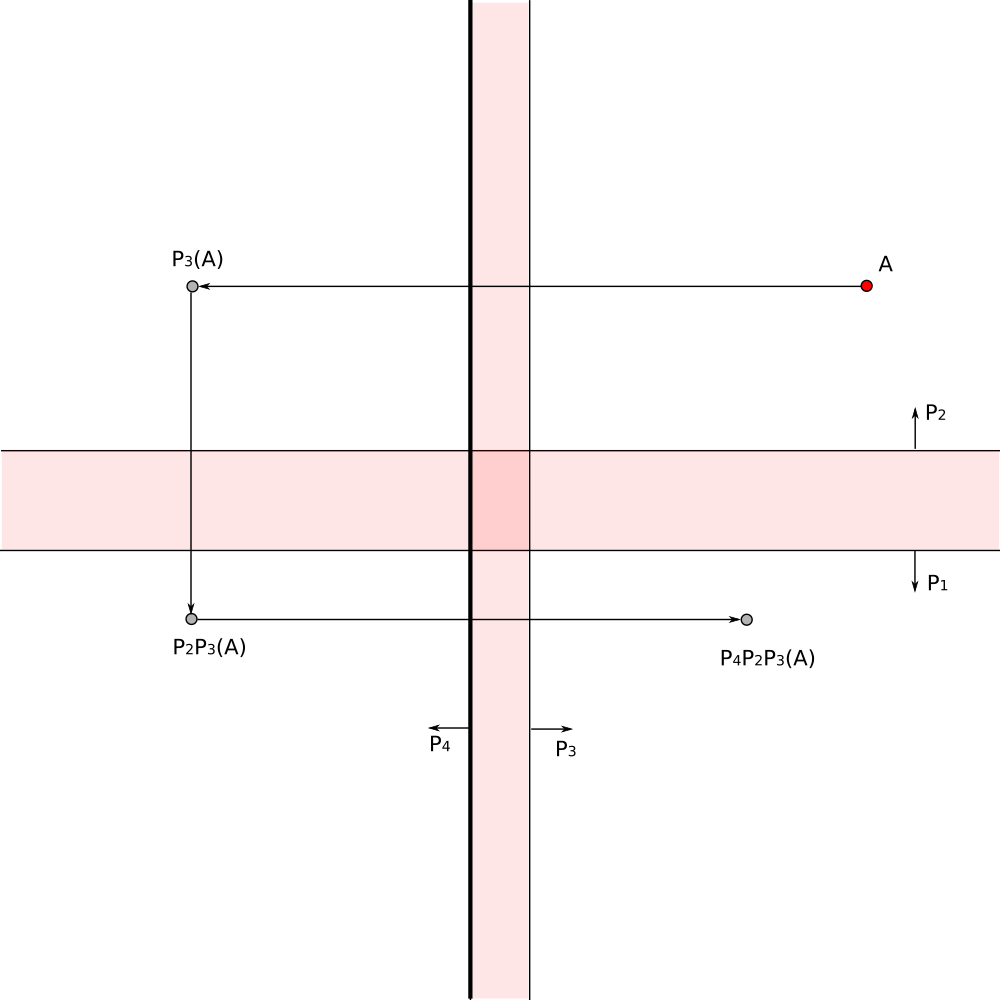
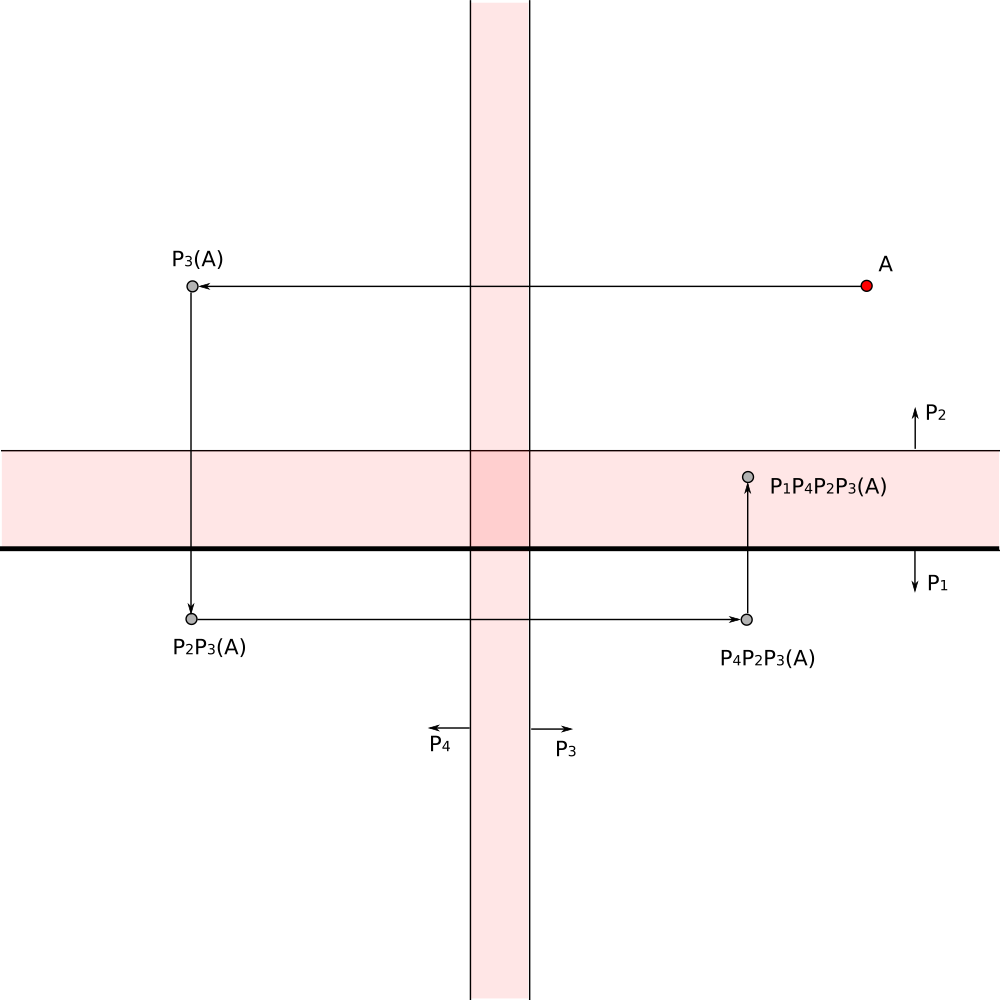
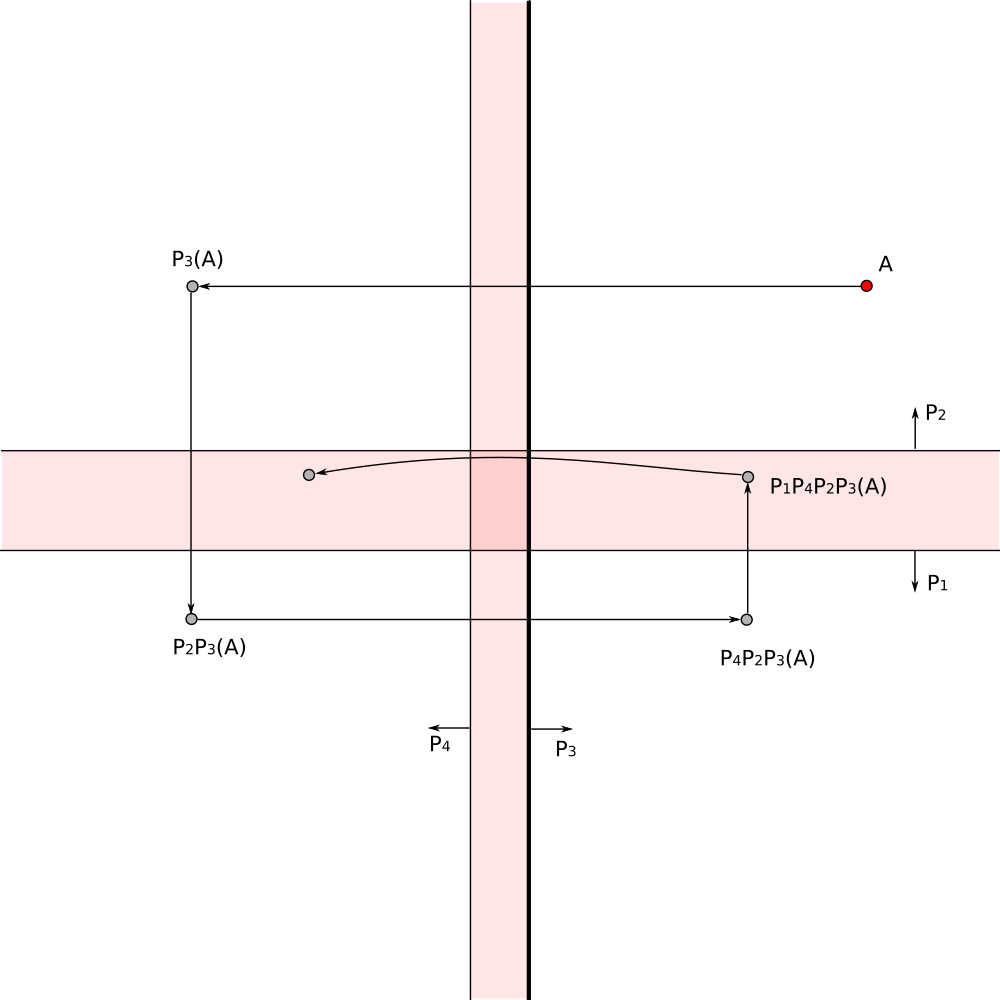
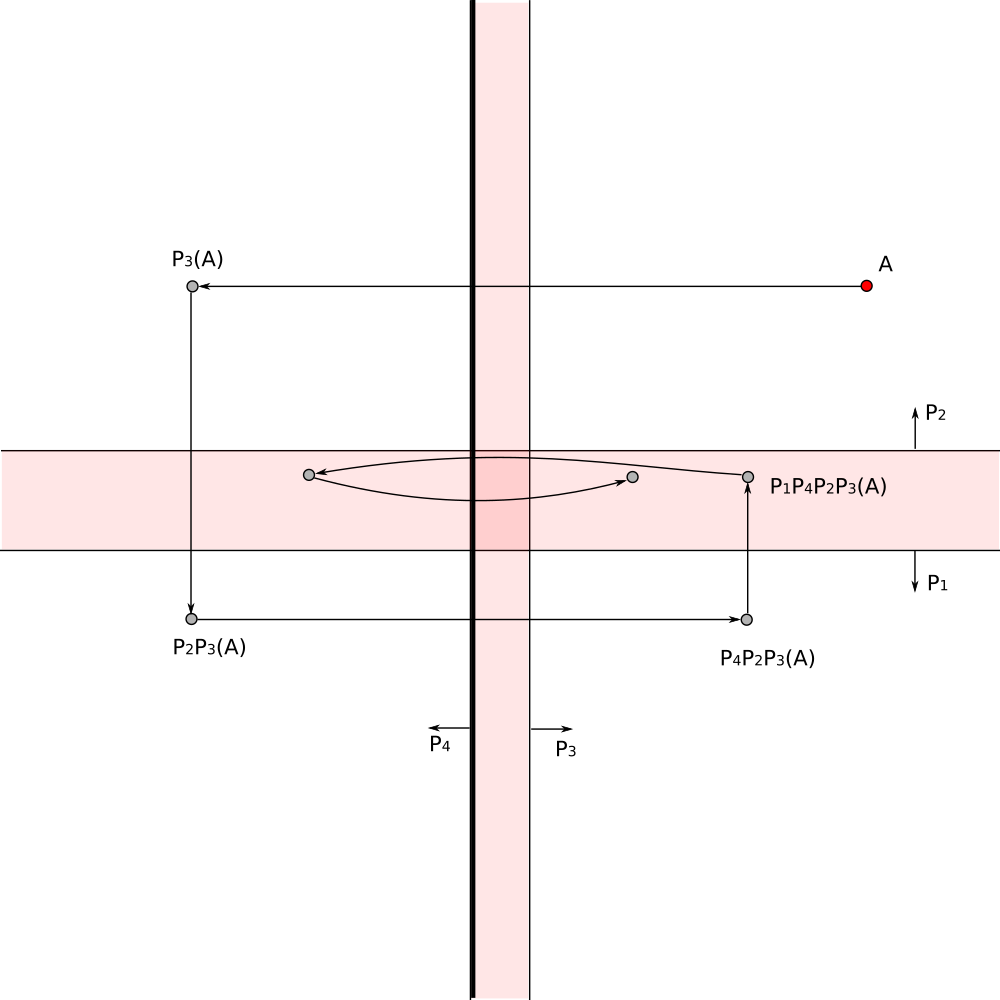
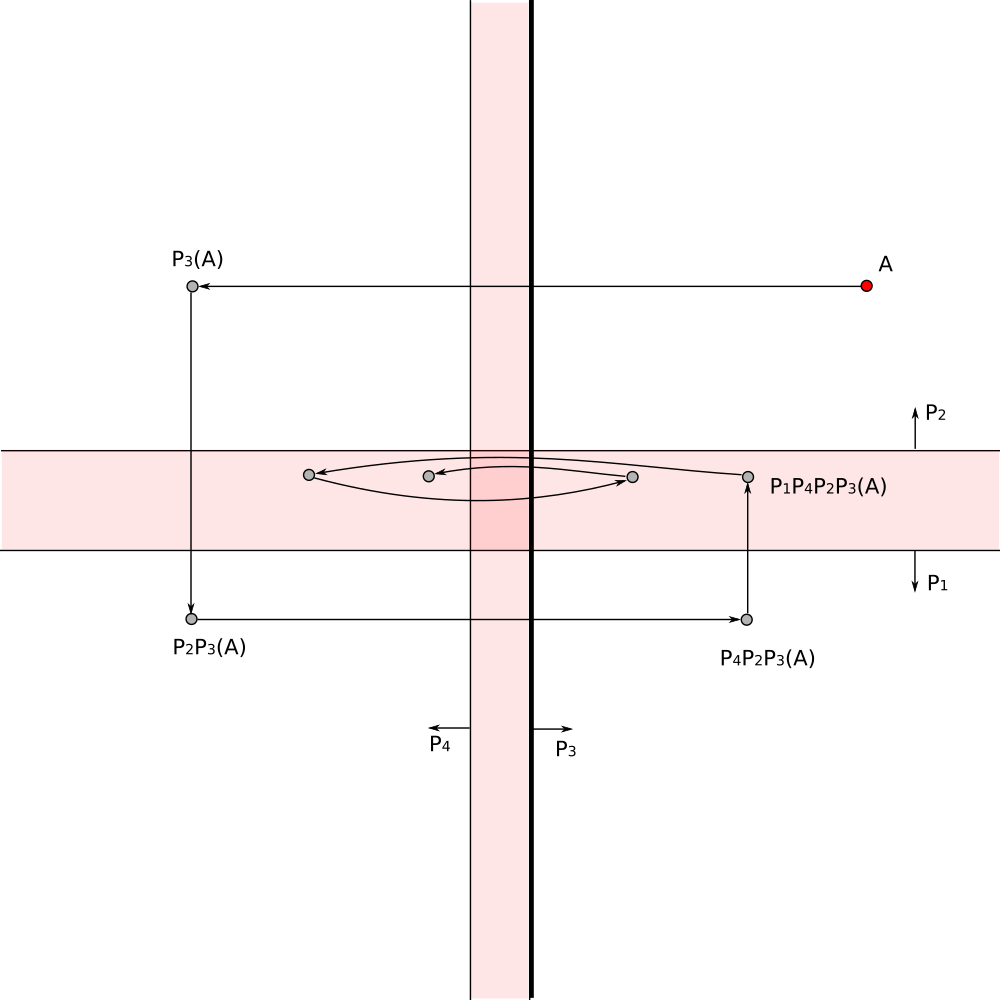
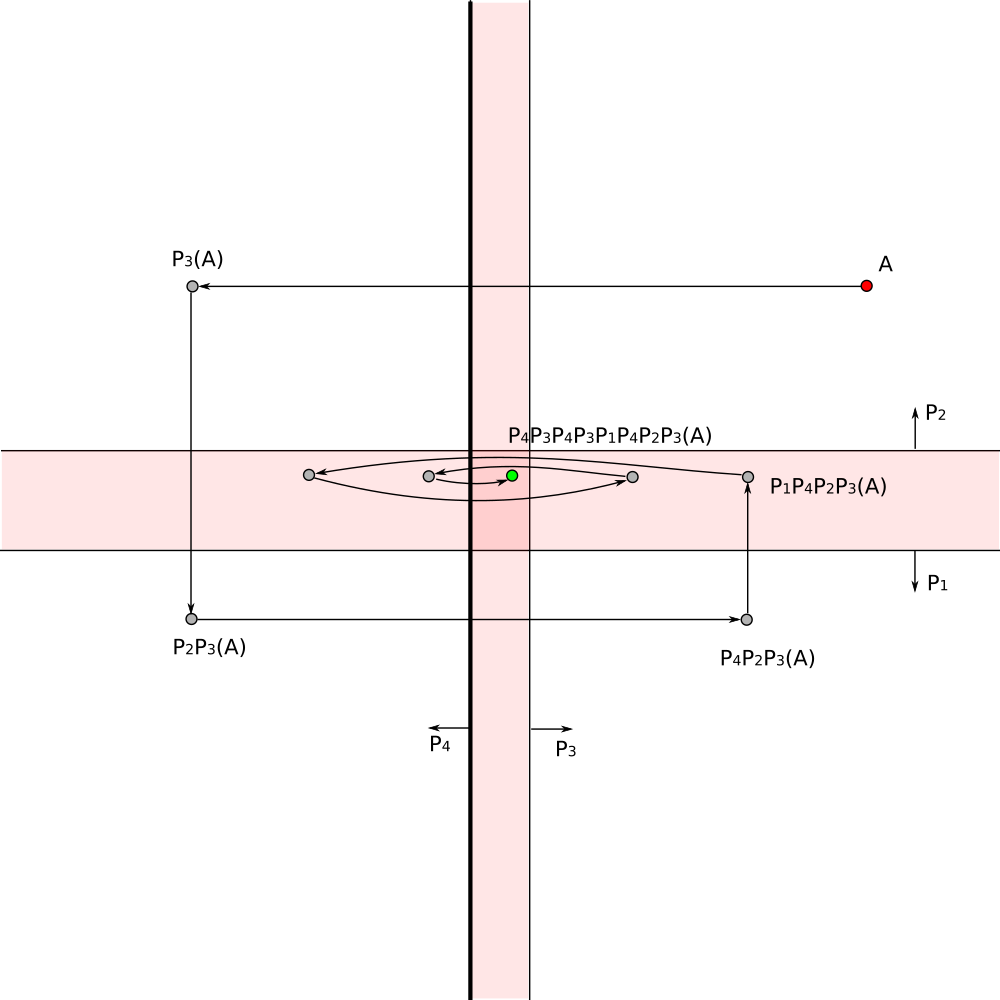

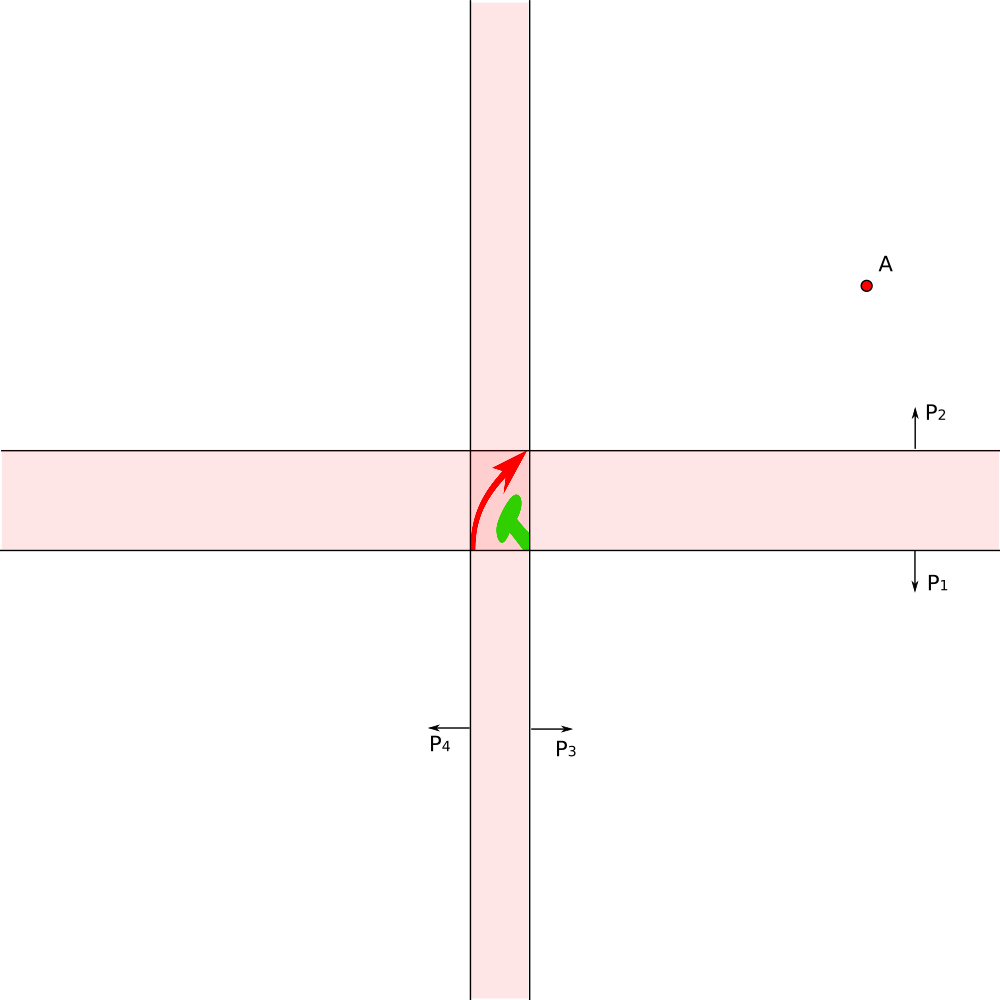
The composition of reflections gives the required transformation
Arbitrary pattern can be placed inside of the fundamental domain

Arbitrary pattern can be placed inside of the fundamental domain
The pattern is reflected to the whole visible space
The calculations for each pixel are independent and can be run on GPU in paralel in real time

Another way to color the pixel is coset coloring.
Here pixels are assigned different color according to coset of the orientation preserving subgroup of index 2.
In this simplest case coset coloring can be obtained by counting number of reflections needed to map pixel to fundamental domain and assigning one color if count is even and another color if count is odd.

Color count equals to the index of subgroup.

Color count equals to the index of subgroup.
The index of subgroup of infinite group can be arbitrary large.
This is coset coloring with 10 colors
Simplest hyperbolic tilings are tiling with tetrahedra.
Lets start with specific example.
Hyperbolic tetrahedron with all finite vertices.
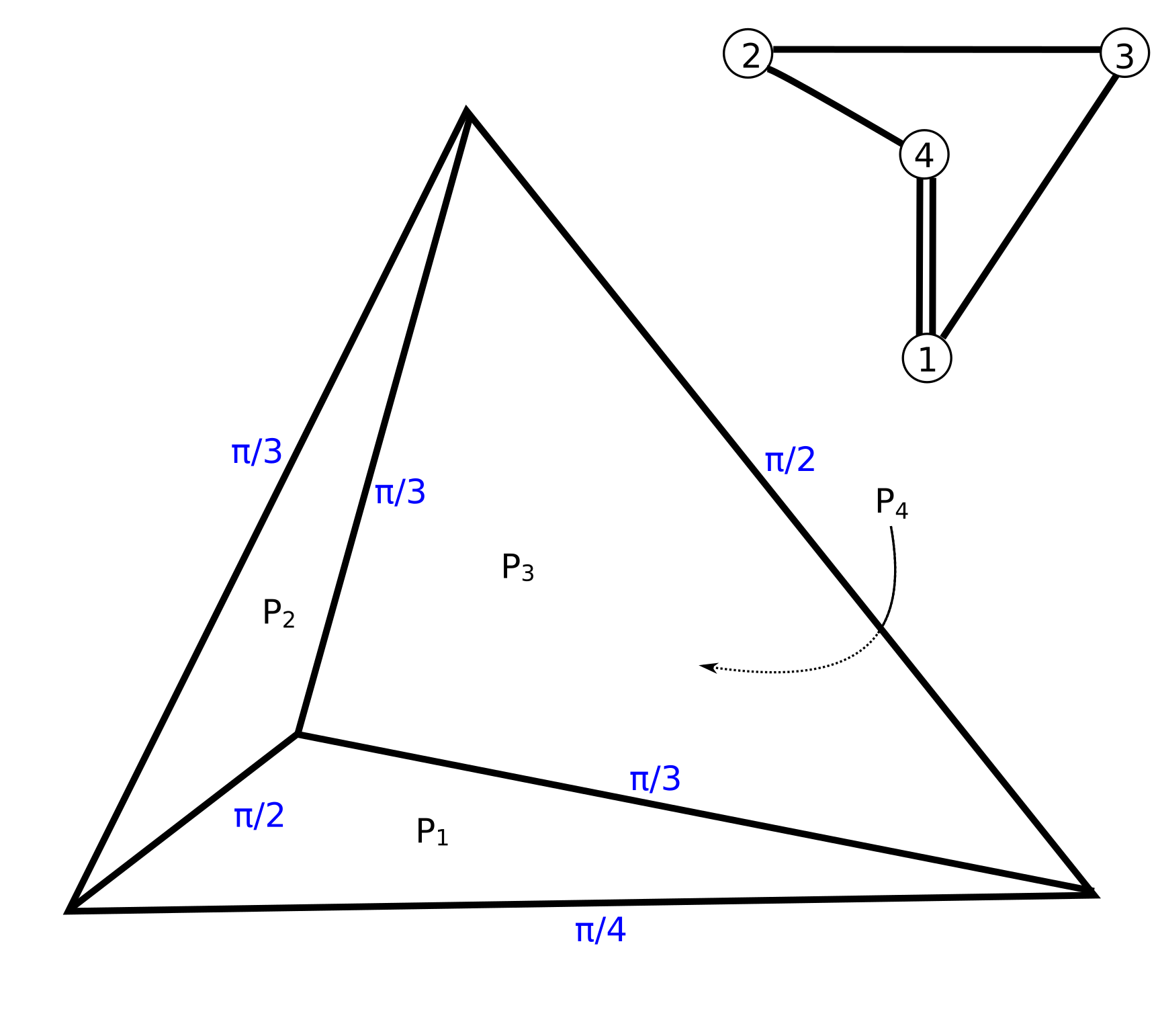
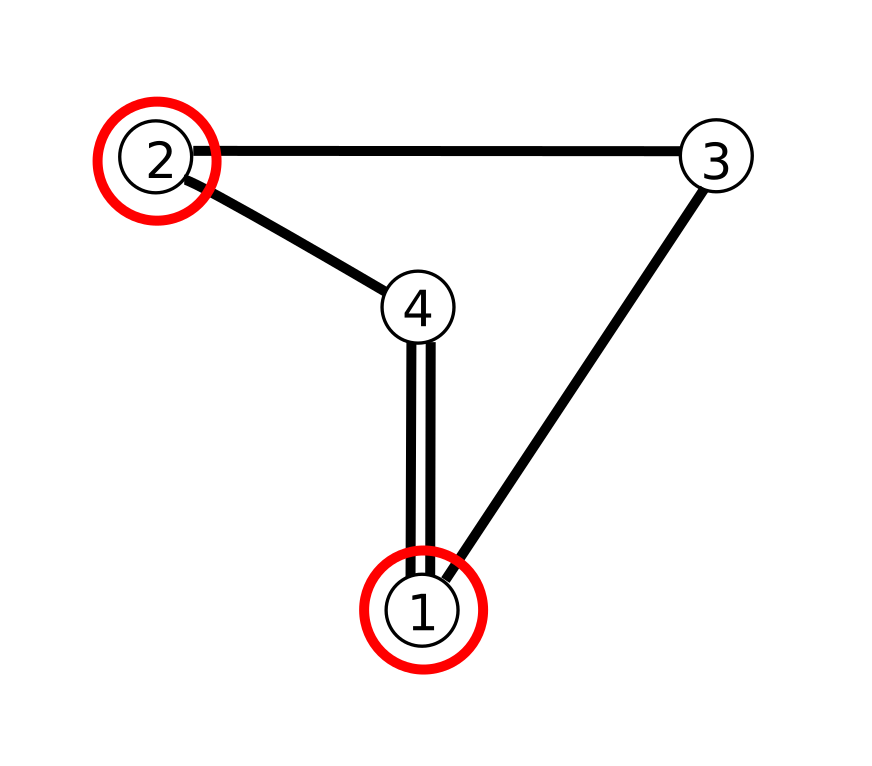
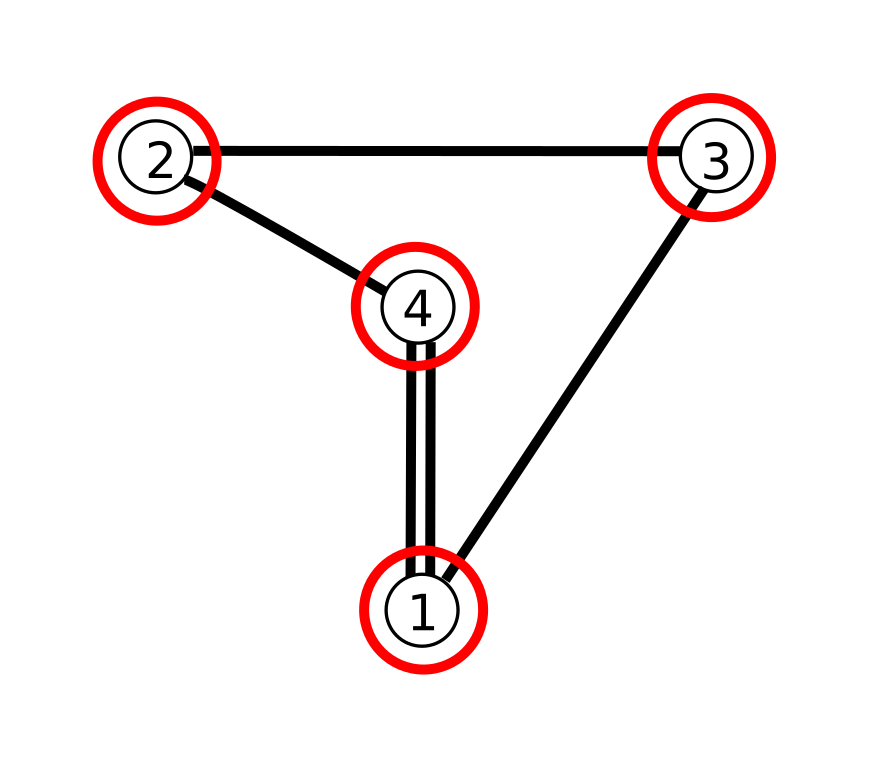
It is convenient to display tetrahedra using Coxeter diagram.
Each plane is shown as small circle.
For each pair of faces `(i,j)` with dihedral angle `alpha = pi/m_(ij)` the corresponding pair of circles `i,j` is connected with `(m_(ij)-2)` lines.
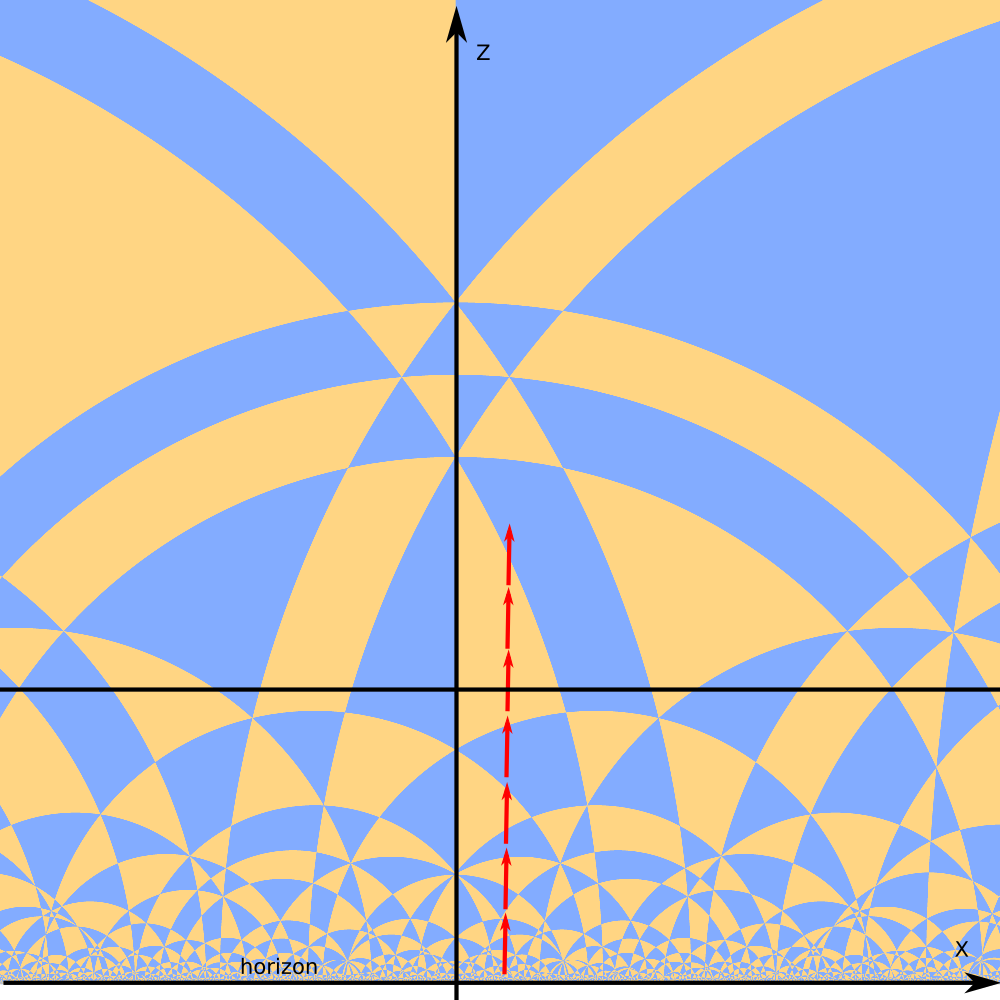
Let's work in the upper half space model of `H^3`. Horizon of `H^3` lies in the xy-plane `(z = 0)`
Lets place planes `P_1` and `P_2` orthogonal to Z axis and orthogonal to each other.
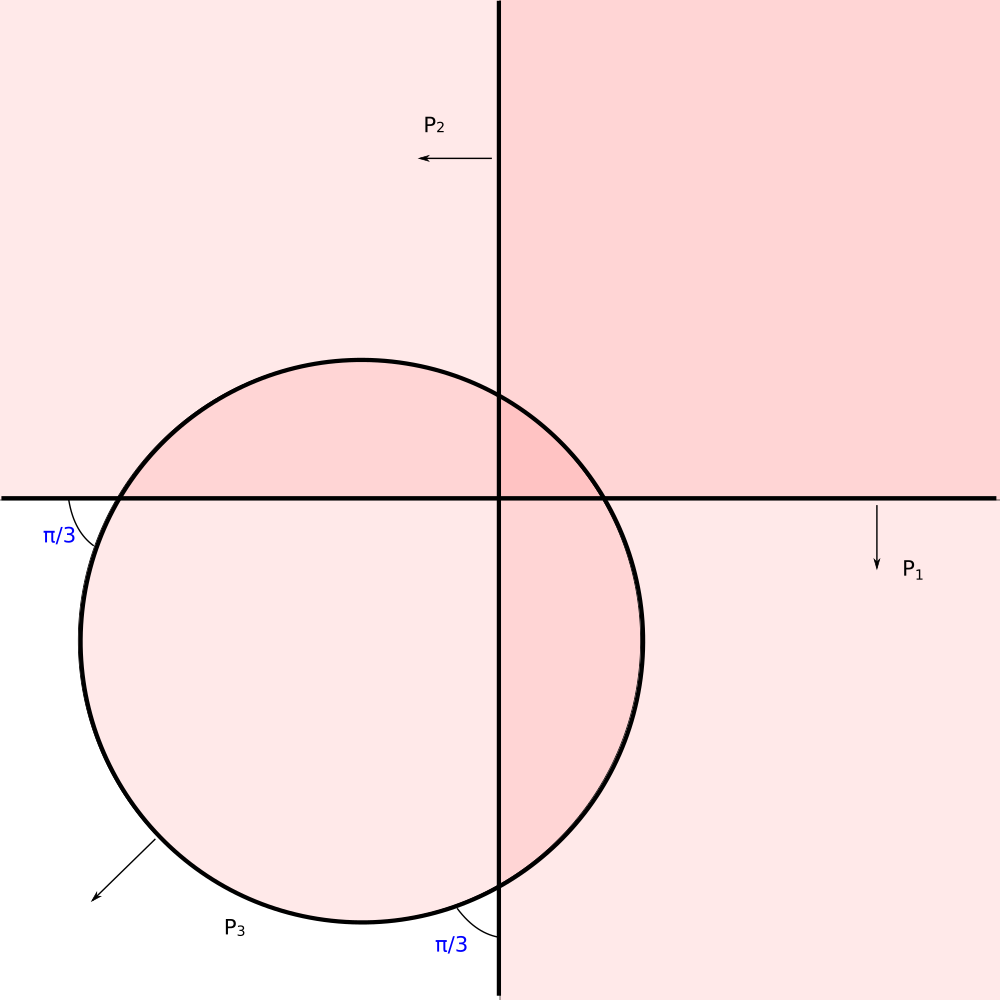
Plane `P_3` is a sphere centered at the horizon.
Dihedral angles of its intersections with planes `P_1` and `P_2` are `alpha_(13) = pi/3` and `alpha_(13) = pi/3`.
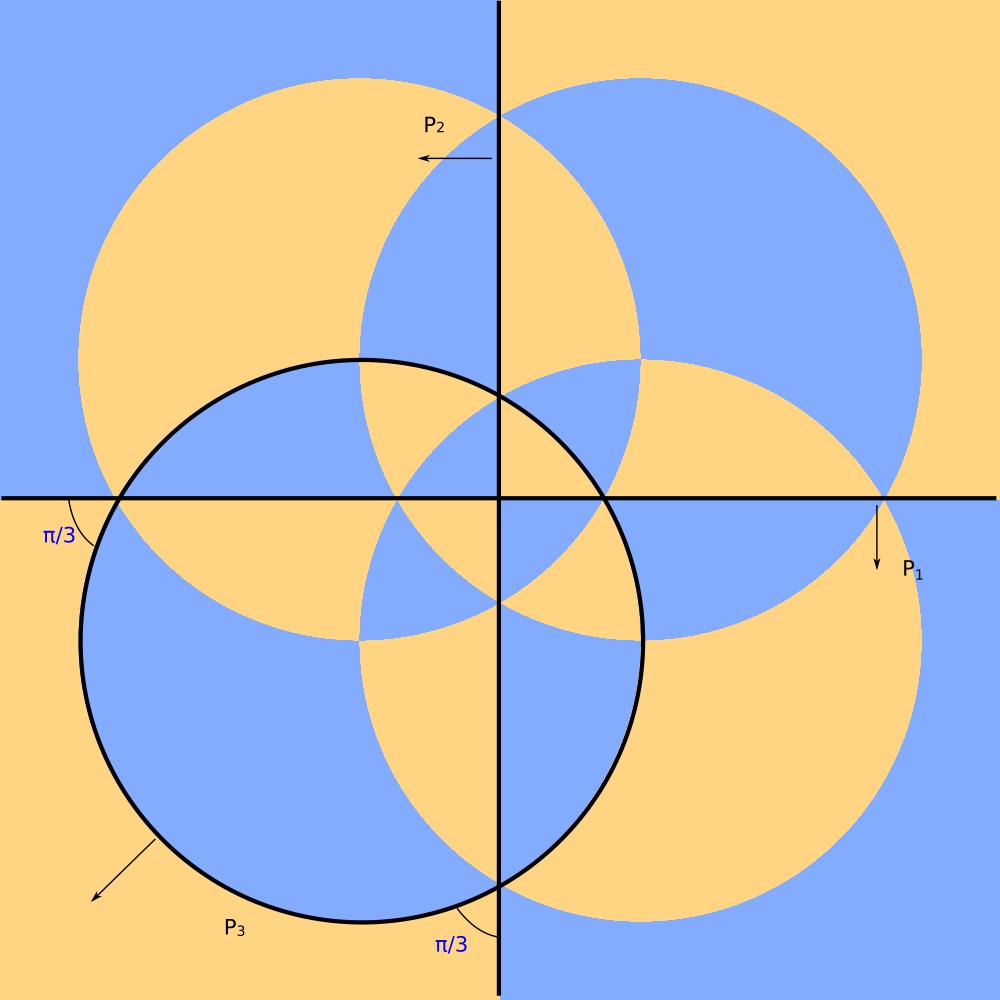

Tiling generated by splanes `P_1` `P_2` `P_3`.
It is stereographic projection of the spherical tiling `**332`.
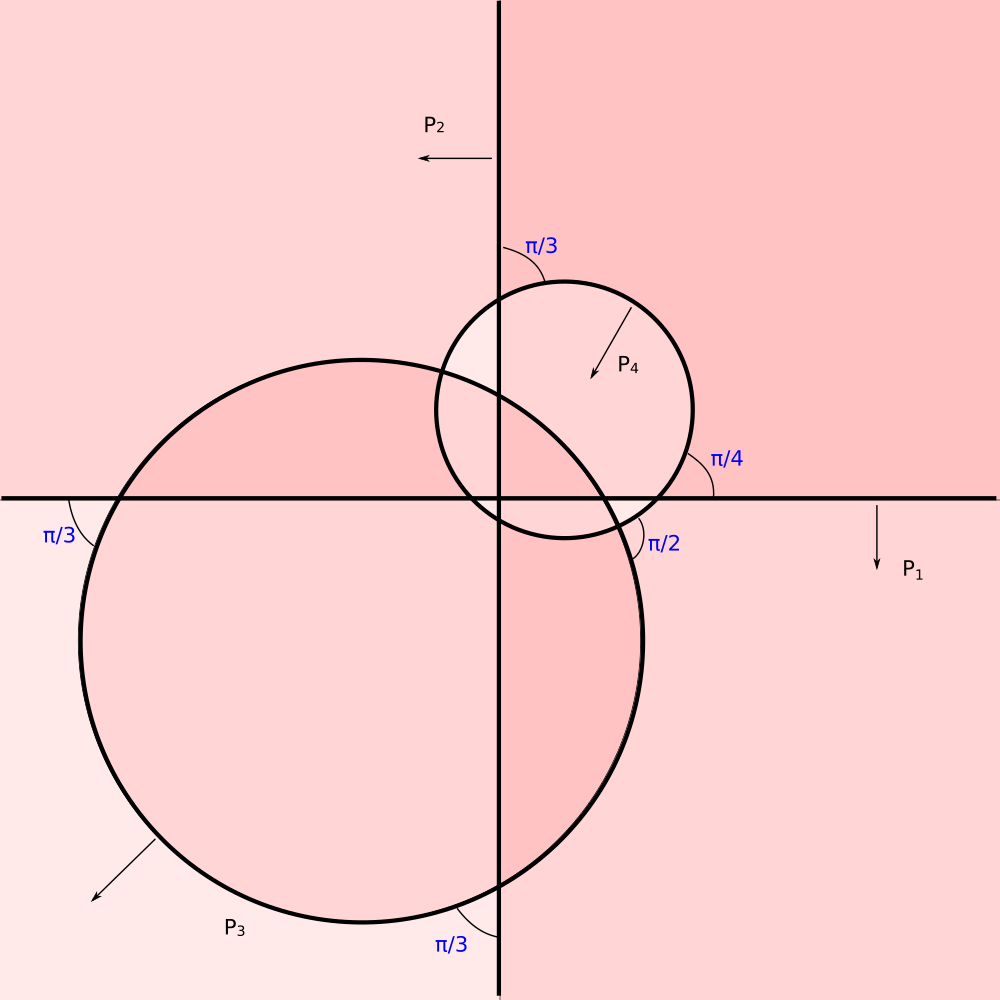
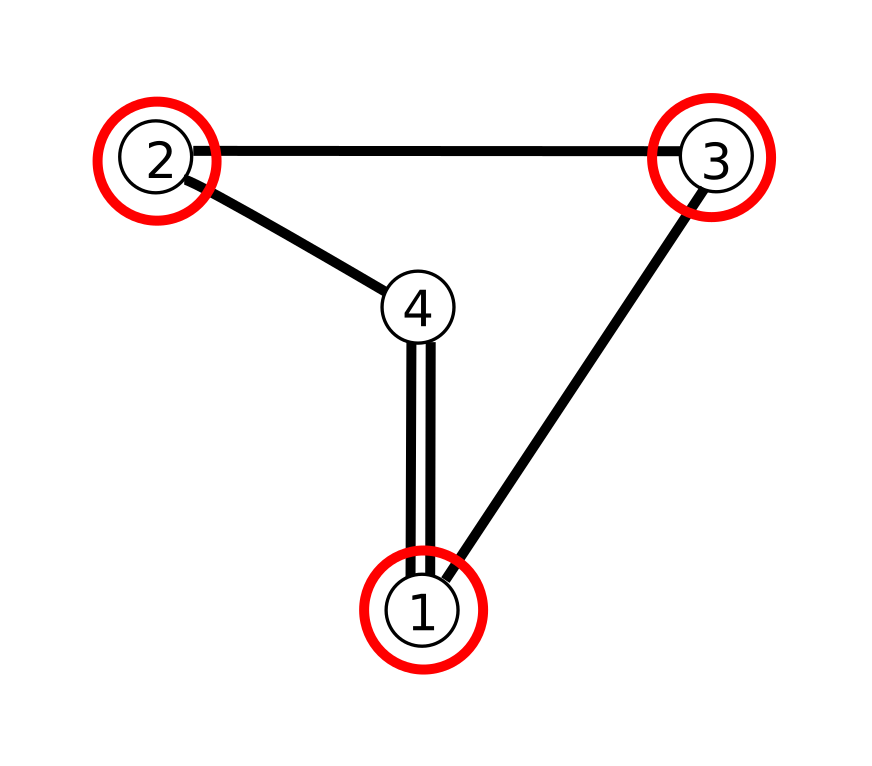
Fourth sphere `P_4` with dihedral angles `alpha_(41) = pi/4` `alpha_(42) = pi/3`, `alpha_(43) = pi/2` finishes the hyperbolic tetrahedron.
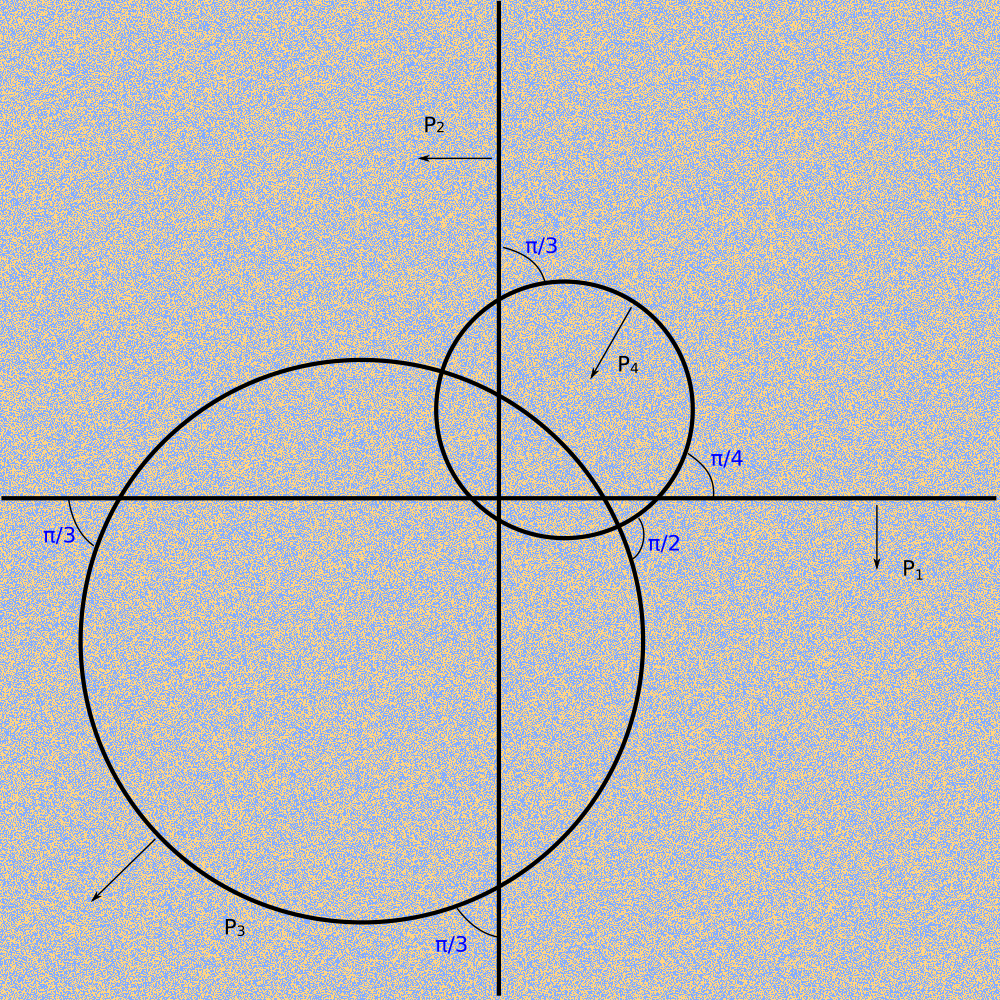

Here is the tiling.
What is going on?

This is the tiling.
What is going on?
We are looking in the wrong place!
Plane `z = 0` is the horizon (infinity) of `H^3`.
Tiles become infinitely small at the horizon.
The visible noise is due to finite precision of calculation.
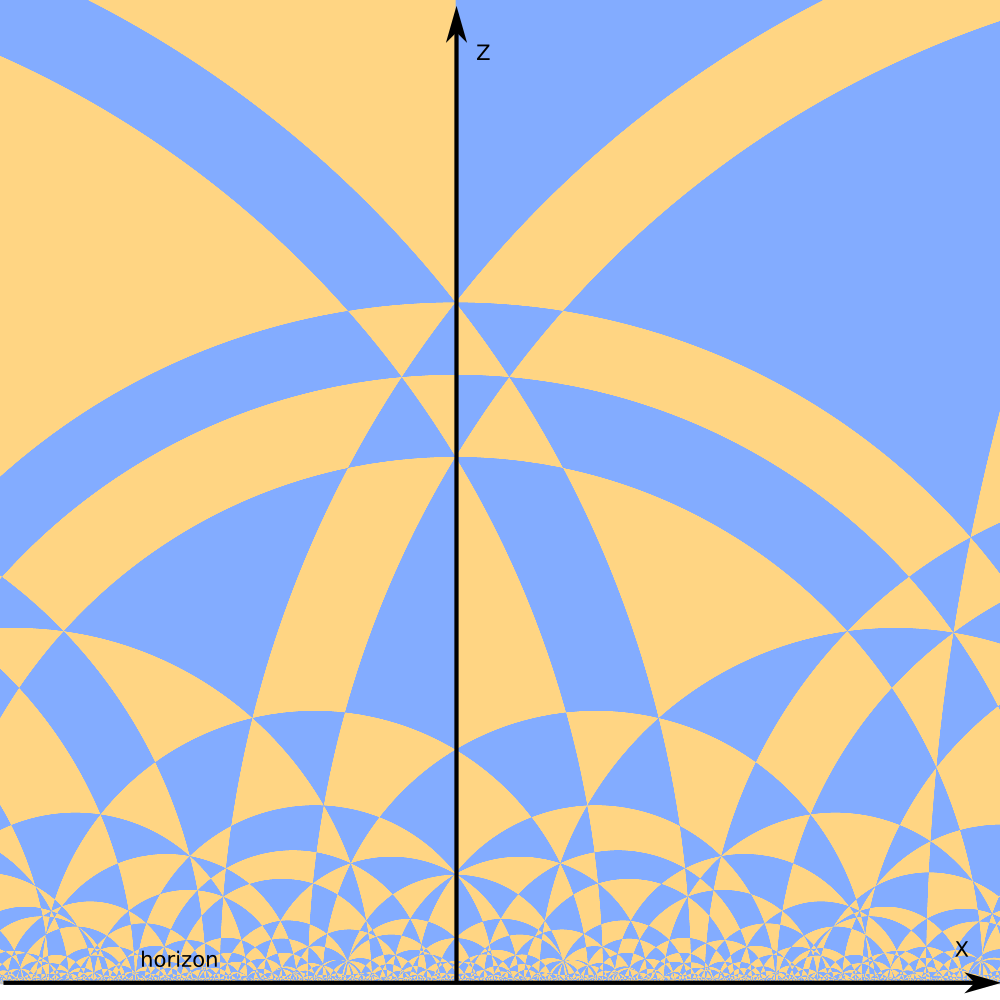
"Right" places to look at the space tiling are hyperbolic planes.
One kind of hyperbolic planes in the upper half space model are planes orthogonal to the horizon.
The image looks similar to 2D tiling of hyperbolic plane in the upper half plane model of `H^2`.
However the polygons are not 2D tiles, but odd shaped slices of 3D tiles by hyperbolic plane.

Another type of hyperbolic planes are half spheres centered at the horizon (image below). The planes can be flattened by stereographic projection.
The flattened tiling (on the left) looks similar to the 2D tilings in the Poincare circle model of `H^2`.
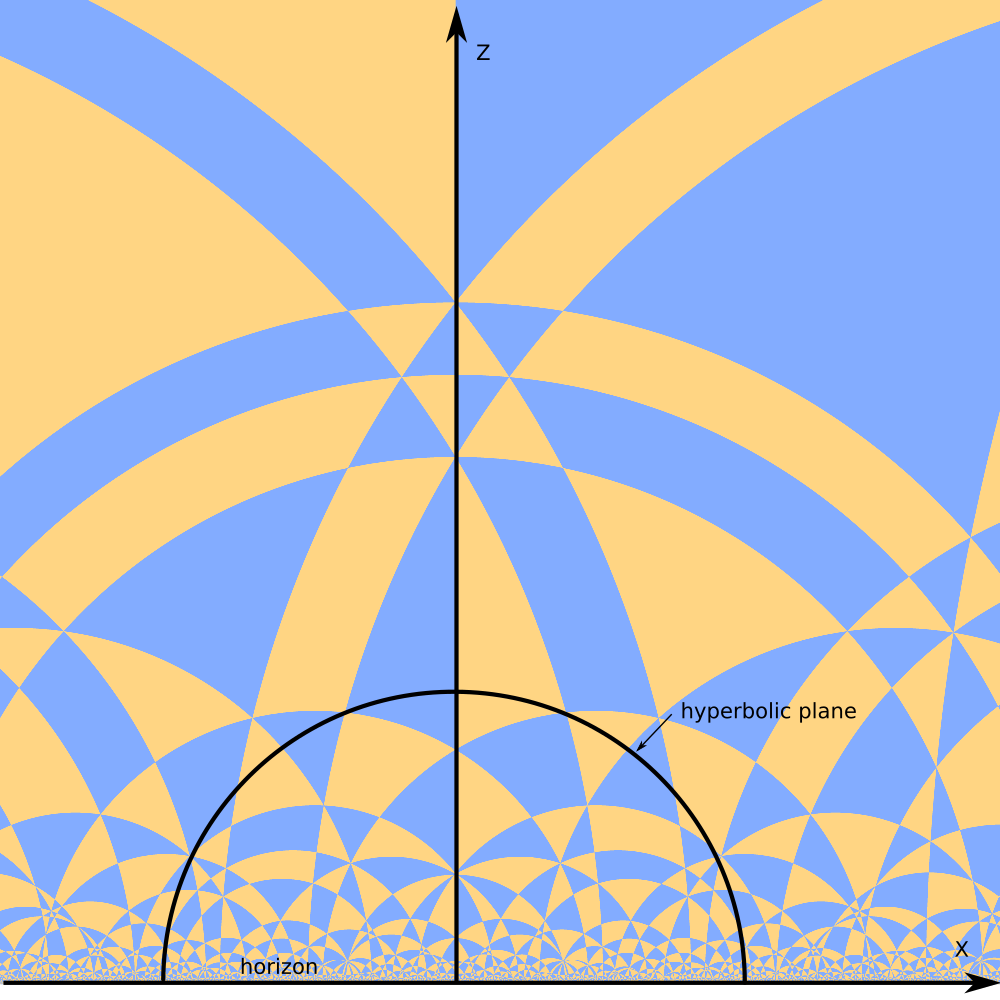
The main feature of hyperbolic tilings visualization is high range of visual scale.
In the circle model of `H^2` we have few regular sized tiles near the center. Tiles shrink rapidly as we approach the horizon.
Upper half plane model `H^2` has similar behavior. Tiles shrink rapidly as we approach the horizon and stretch rapidly as we move up.
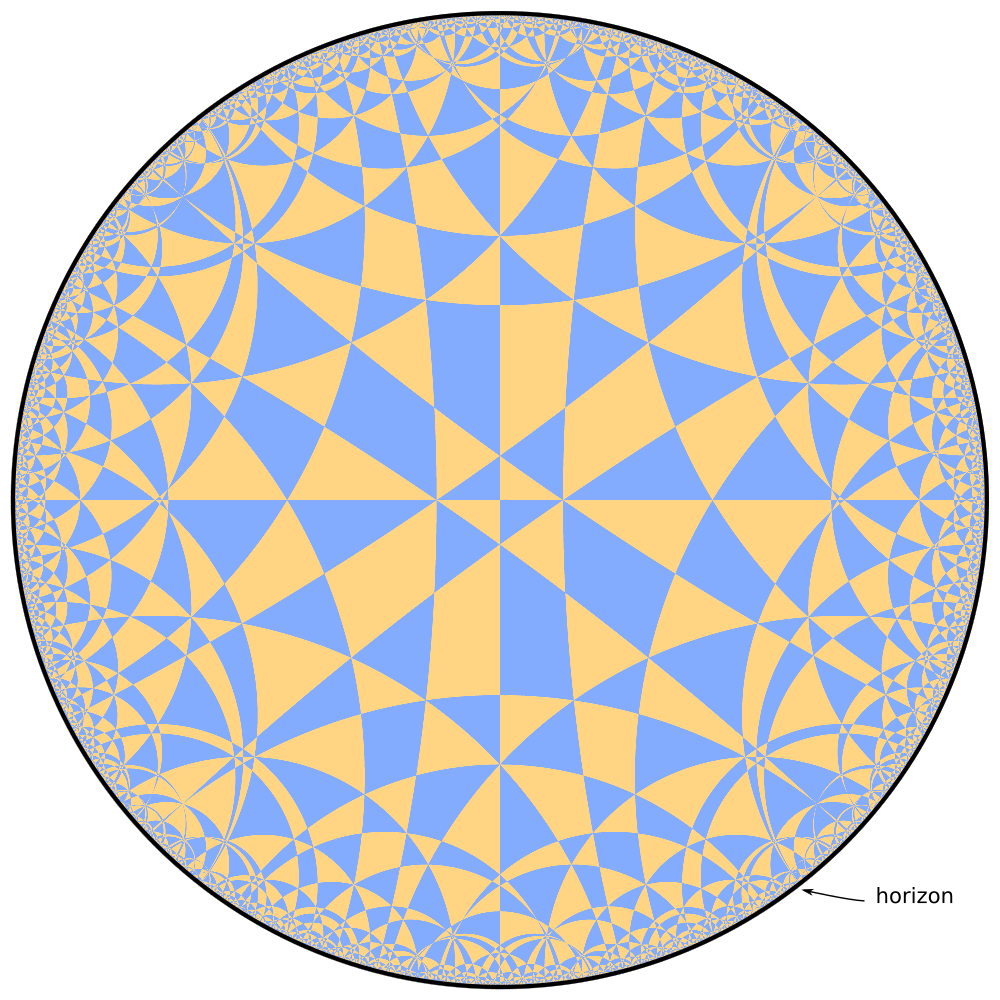

Let's "flatten" the hyperbolic plane.
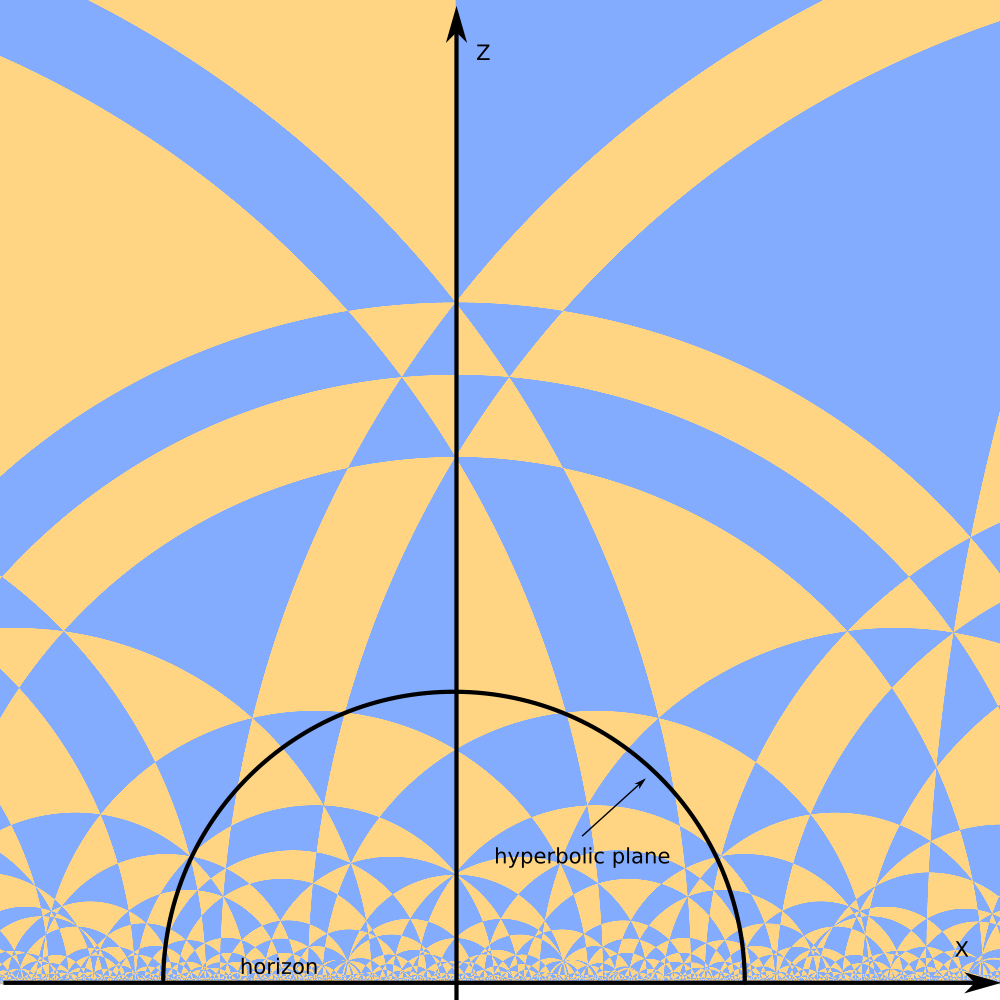

Let's "flatten" the hyperbolic plane.
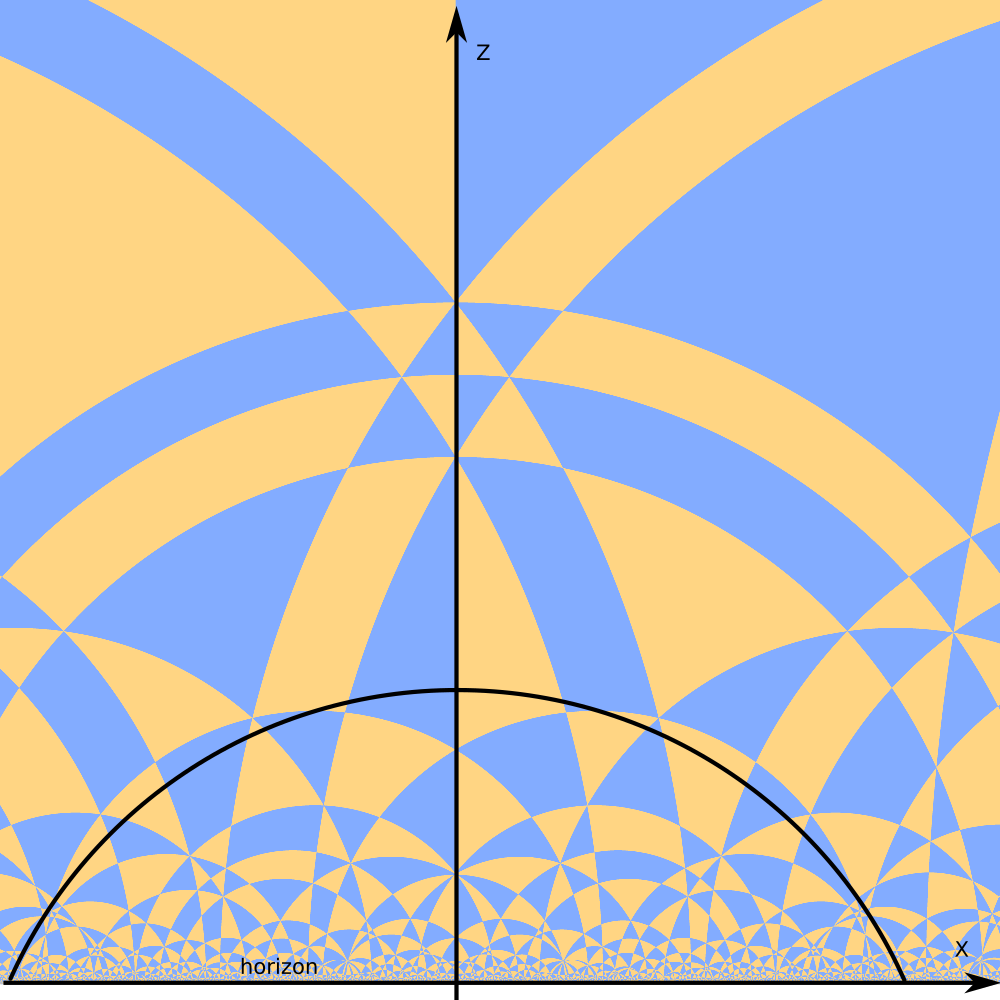

Let's "flatten" the hyperbolic plane.
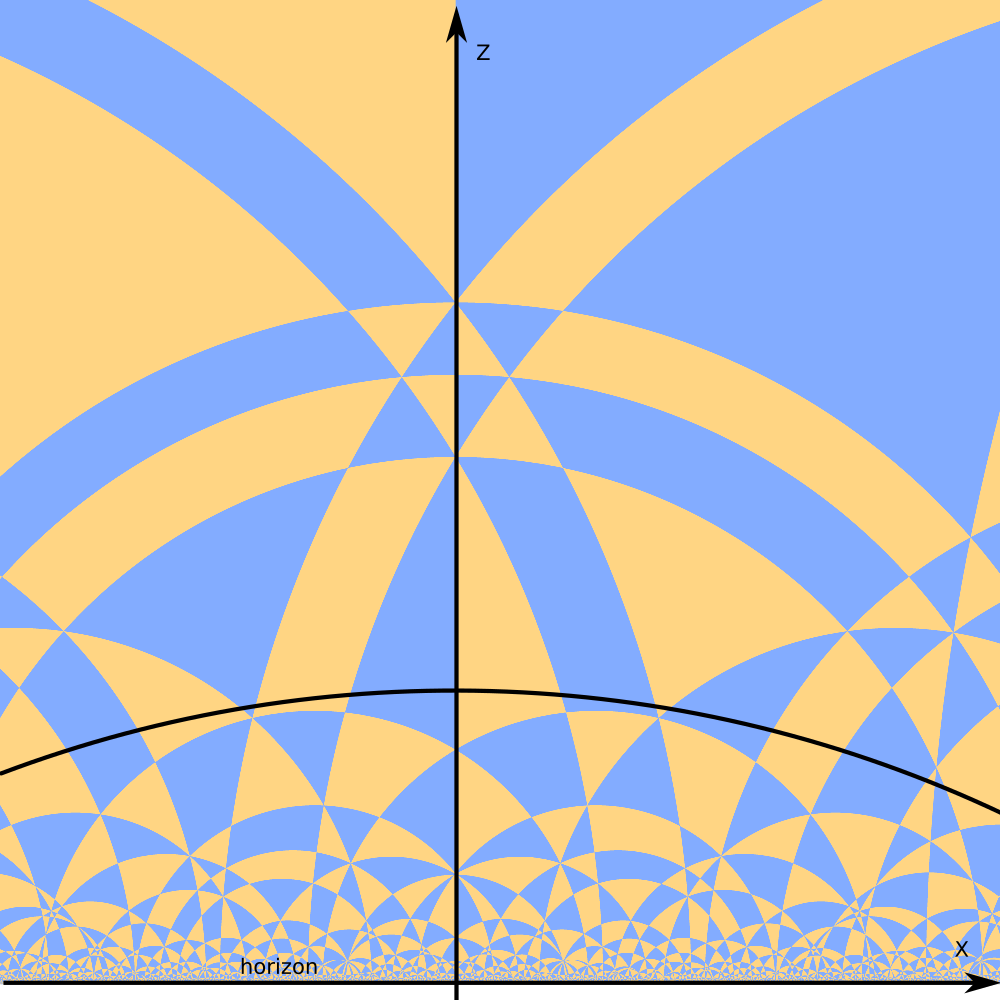

We got horosphere.
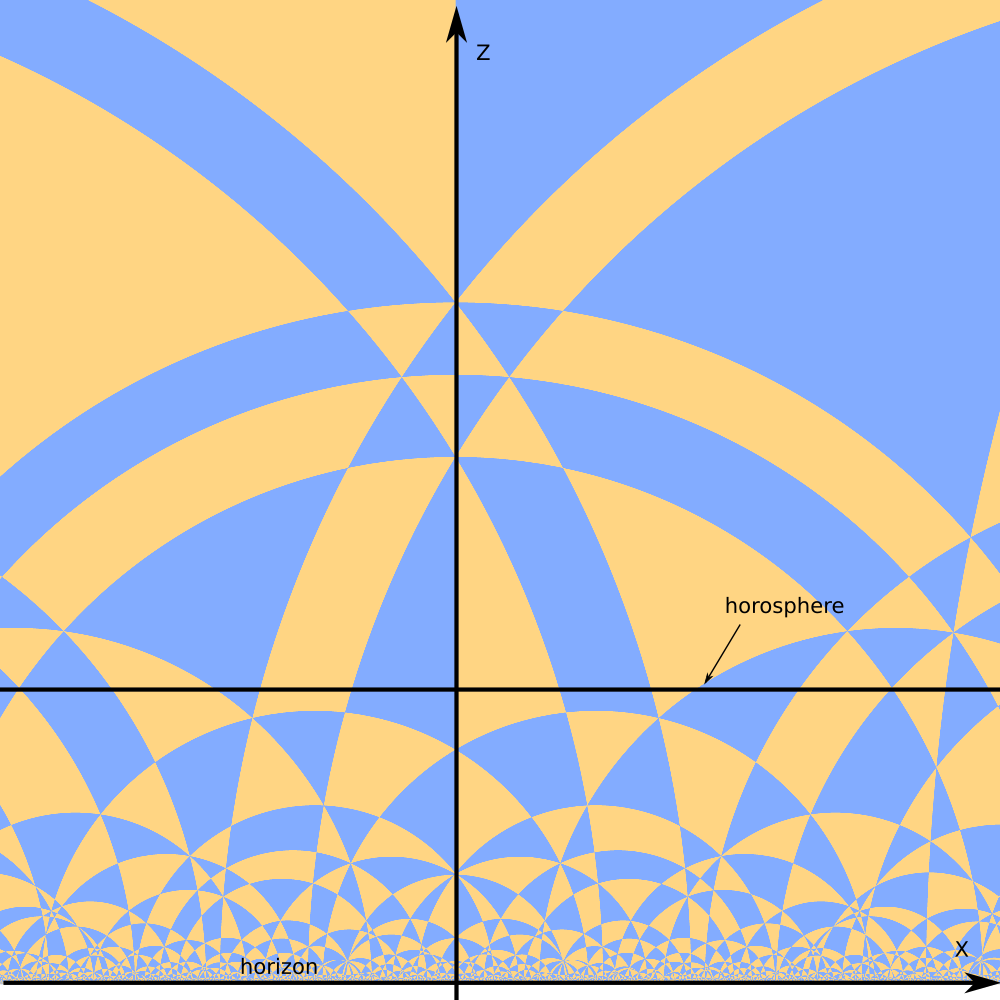

Zooming out the camera.


Zooming out the camera.


Zooming out the camera.


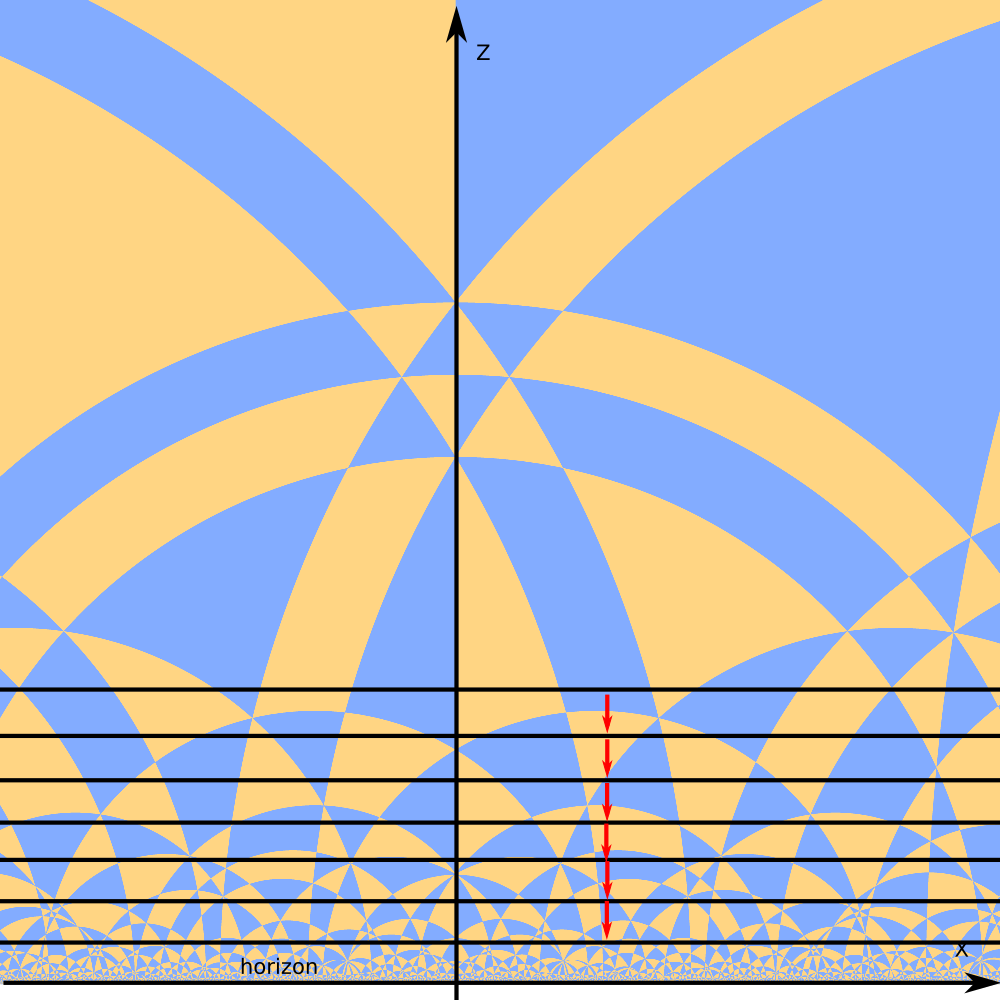
There are different motion we can perform with horospere
Straight hyperbolic translation.
Animaton
https://youtu.be/PKauqA_Qp9Q
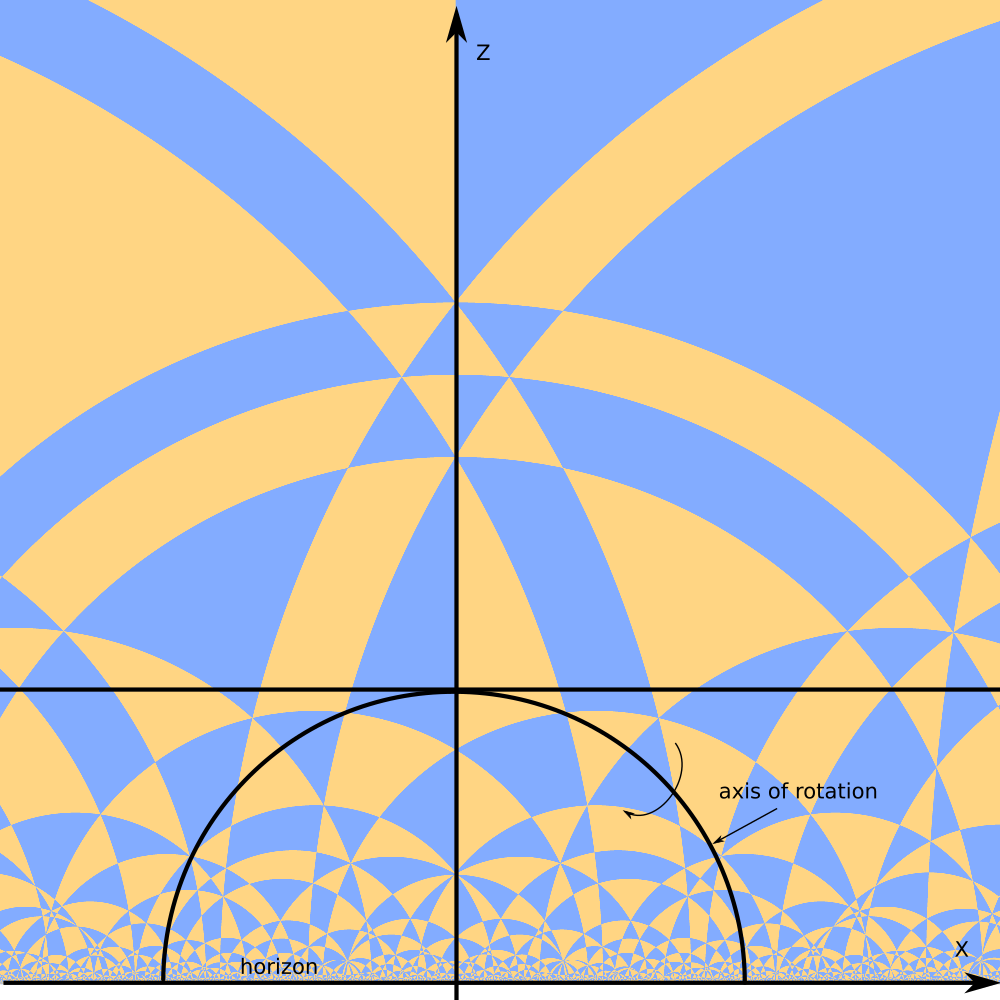
There are different motion we can perform with horospere
Hyperbolic rotation around hyperbolic straight line.
Animaton 1.
https://youtu.be/PhcbmsTYc-0
animaton 2.
https://youtu.be/rSEzGtp56vI
There are different motion we can perform with horospere
Moving tiling past horosphere.
Similar to horosphere hyperbolic translation.
The difference is that scale of the tiling remain the same.
Animation.
https://youtu.be/gGvlkomzvAg
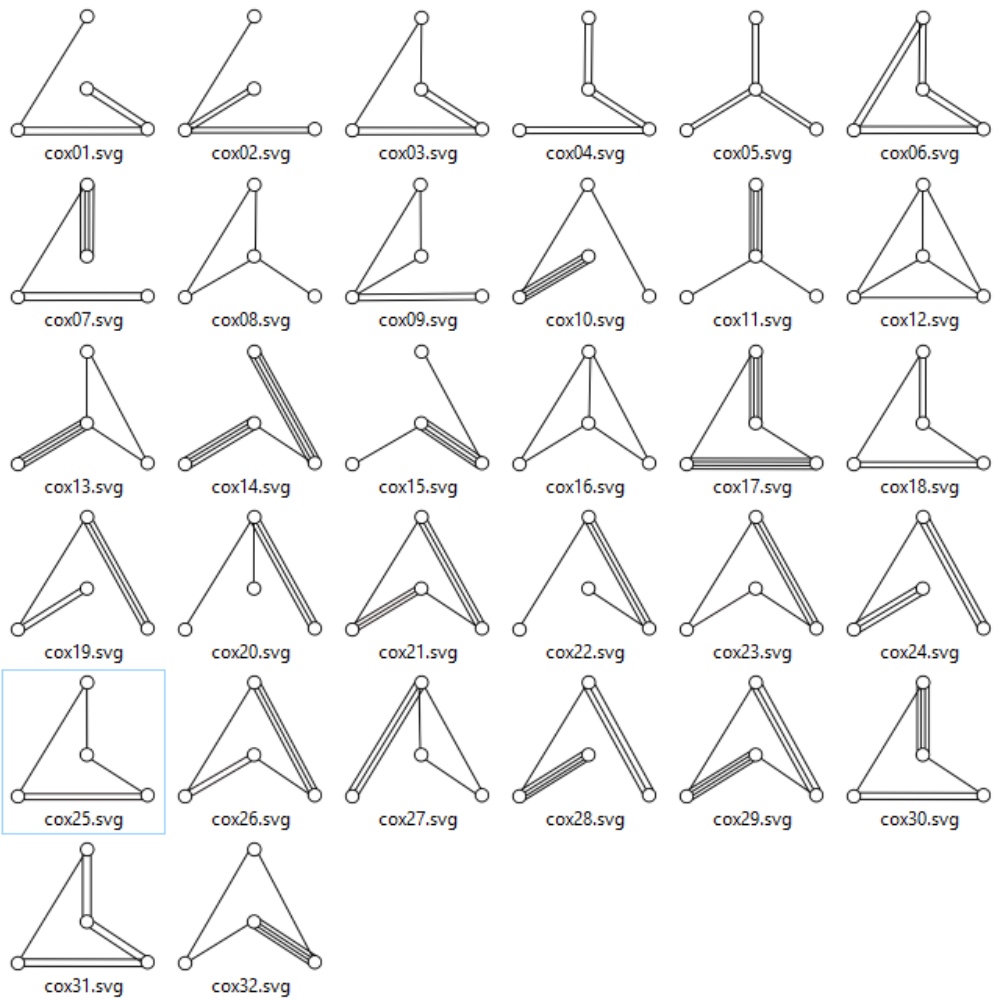
There are 32 compact hyperbolic tetrahedra with kaleidoscopic angles.
There is infinite number of non compact tetrahedra (tetrahedra with vertices beyond infinity).
There is infinite number of more complex polyhedra.
A lot of possibilities for fun.

This tetrahedron has icosahedral vertex `**532` and ideal vertex `**333`.
Animation.
https://youtu.be/AVnNs3dU3-c

Tetrahedron has ideal vertex `**333`.
Horosphere is moving away from that vertex.
Animation.
https://youtu.be/F1cDHtS6oeE
Slicing euclidean tiling wih plane also produces interesting results

Animation 1
https://youtu.be/tR_IFchXvo8

3D printing involves creation of spherical color map and applying it to a shape (sphere).
The modeling was done in ShapeJS - online tool for making 3d printable models via script.
The 3D printing was done by Shapeways.


WebGL is web browser API which allow web pages run graphics program directly on users GPU (graphics card).

Online adress of the talk
http://bulatov.org/math/180110/