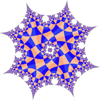

Bridges Conference
Online address of the talk:
bulatov.org/math/1107/

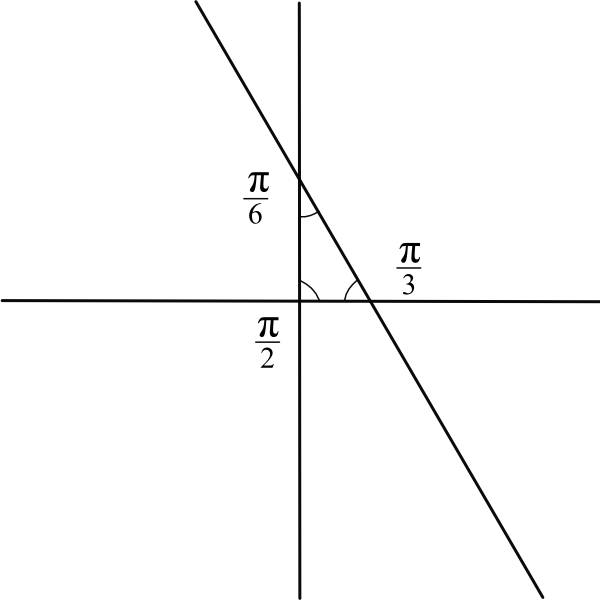
Let's put 3 reflection lines in the plane.
Angles between the lines are fractions of `pi`:
`pi/2` , `pi/3` , `pi/6`
Triangle inside of intersection is fundamental domain of kaleidoscope.
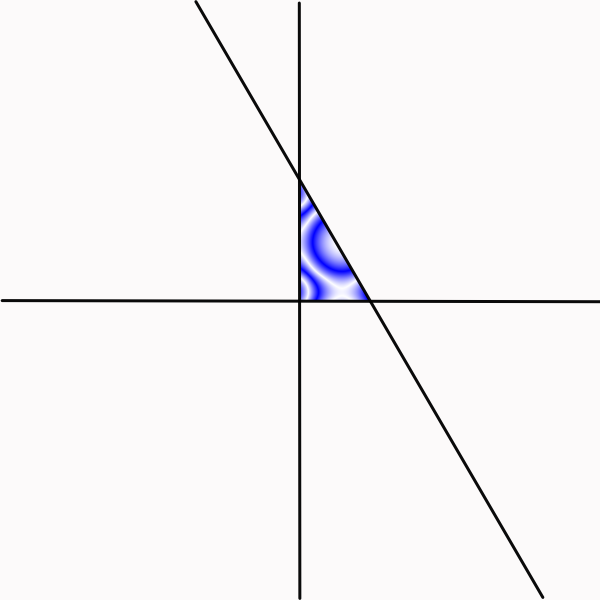
Let's place arbitrary pattern inside of fundamental domain.

And apply all possible reflections in the mirrors.
Symmetry of this pattern is *236.

There are only 4 different kind of euclidean kaleidoscopes.
*236

There are only 4 different kind of euclidean kaleidoscopes.
*244

There are only 4 different kind of euclidean kaleidoscopes.
*333

There are only 4 different kind of euclidean kaleidoscopes.
*2222

*2222 kaleidoscope is formed by 4 reflection lines. Fundamental domain is rectangle.
It has extra degree of freedom - aspect ratio of rectangle.

*2222 kaleidoscope is formed by 4 reflection lines. Fundamental domain is rectangle.
It has extra degree of freedom - aspect ratio of rectangle.

*2222 kaleidoscope is formed by 4 reflection lines. Fundamental domain is rectangle.
It has extra degree of freedom - aspect ratio of rectangle.

*2222 kaleidoscope is formed by 4 reflection lines. Fundamental domain is rectangle.
It has extra degree of freedom - aspect ratio of rectangle.

*2222 kaleidoscope is formed by 4 reflection lines. Fundamental domain is rectangle.
It has extra degree of freedom - aspect ratio of rectangle.
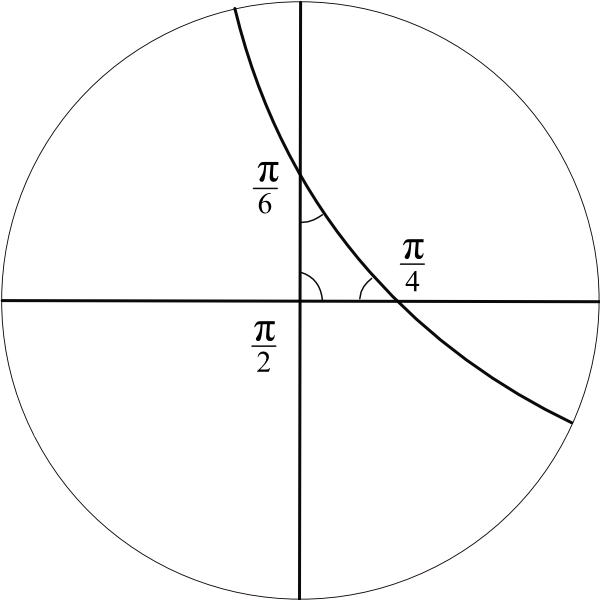
Poincare disc model of hyperbolic plane.
Interior of the unit disk represents the whole hyperbolic plane.
Hyperbolic straight lines are circles (or lines) orthogonal to unit circle.
3 reflection lines in the hyperbolic plane make dihedal angles `pi/2` , `pi/4` , `pi/6`


Place a pattern into fundamental domain


Make one reflection.
Reflections in lines are replaced with inversions in circles.


Make 2 reflections


Make 3 reflections


Make 4 reflections


Make 5 reflections


Make 6 reflections


Make 7 reflections


Make 8 reflections


Make 9 reflections


Make 10 reflections


Make 11 reflections


Make 12 reflections


Make 13 reflections


Make 14 reflections


Make 15 reflections


Make 16 reflections


Make 17 reflections


Make 18 reflections


Make 19 reflections


Make 20 reflections


"Infinite" number of reflections.

Complete hypebolc kaleidoscope *246.

Show different copies of fundametal domain in alternating colors for better view of the "grid" structure.

There are countable number of different triangular kaleidoscopes in the hyperbolic plane.
Angles of triangle should be submultipes of `pi` or `0`
`pi/k`, `pi/l`, `pi/m`, `l,m,n >=2`
Sum should be less than `pi`
`pi/k + pi/l + pi/m < pi`
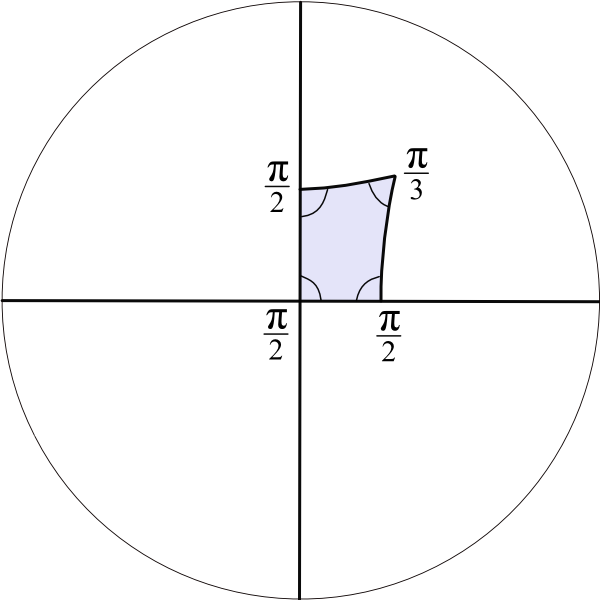
What about other polygons in hyperbolic plane?
Let's make quadrilateral with angles
`pi/2`, `pi/2`, `pi/2`, `pi/3`


Reflect in the sides of this quadrilateral.
1 reflection


2 reflections


3 reflections


4 reflections


5 reflections


6 reflections


7 reflections


8 reflections


9 reflections


11 reflections


13 reflections


15 reflections

Complete *2223 kaleidoscope

Scale x 2.

Scale x 10.

Scale x 50.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Length of one side of *2223 kaleidoscope is free parameter.

Any hyperbolic n-gon with "kaleidoscopic" angles generates kaleidoscope.
Such kaleidoscope has `n-3` free continuous parameters
(lengths of `n-3` sides for example).
Not for all values of parameters such n-gon exists.
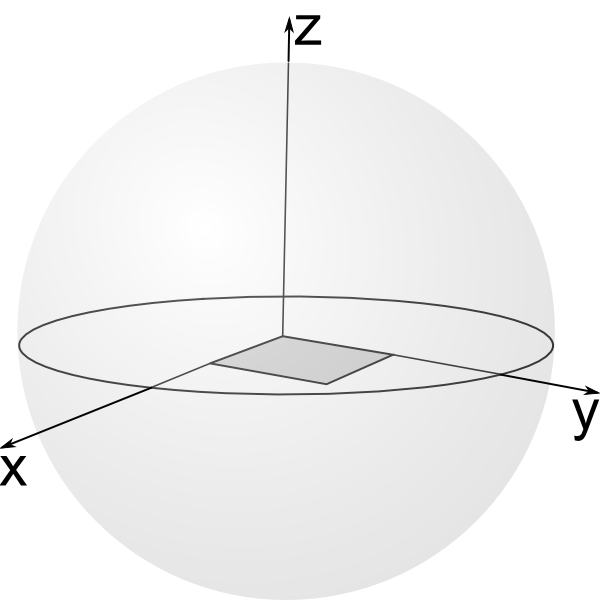
Mapping unit disk to unit sphere. Klein model.
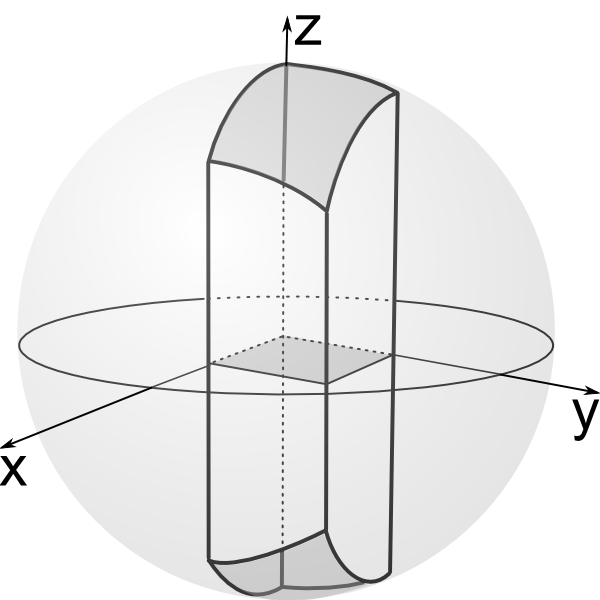
Mapping unit disk to unit sphere. Klein model.
Extend flat quadrilateral in x-y plane into 3-dimensional chimney otrhogonal to x-y plane.
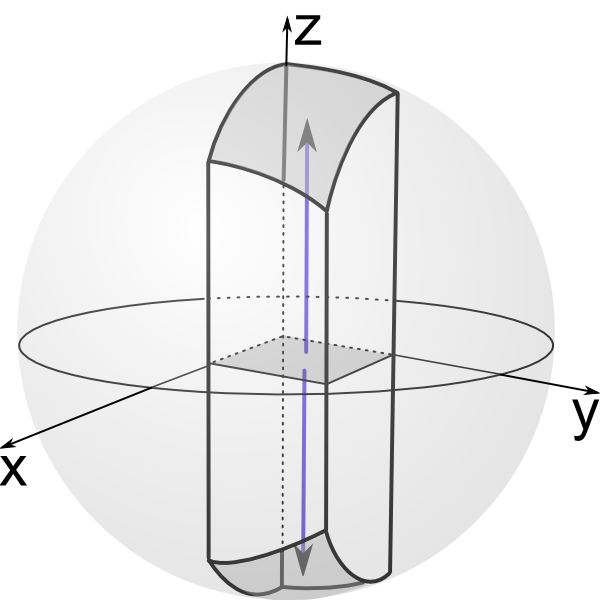
Mapping unit disk to unit sphere. Klein model.
Extend flat quadrilateral in x-y plane into 3-dimensional chimney otrhogonal to x-y plane.
Map quadrilateral into 2 spherical quadrilaterals.
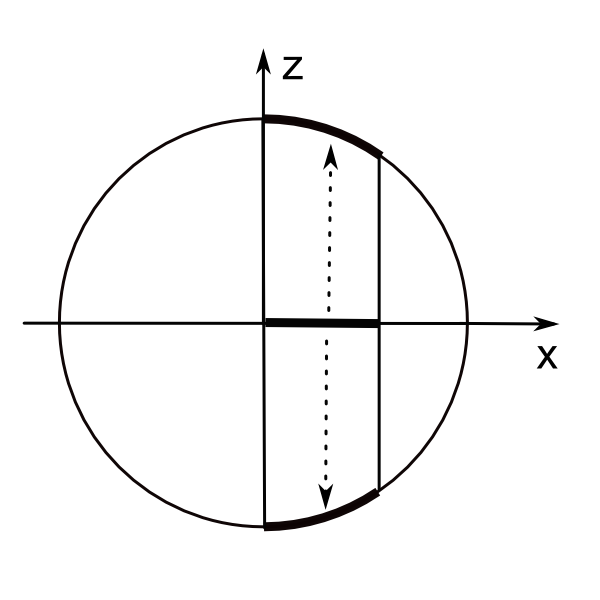
Mapping unit disk to unit sphere, y-axis view.
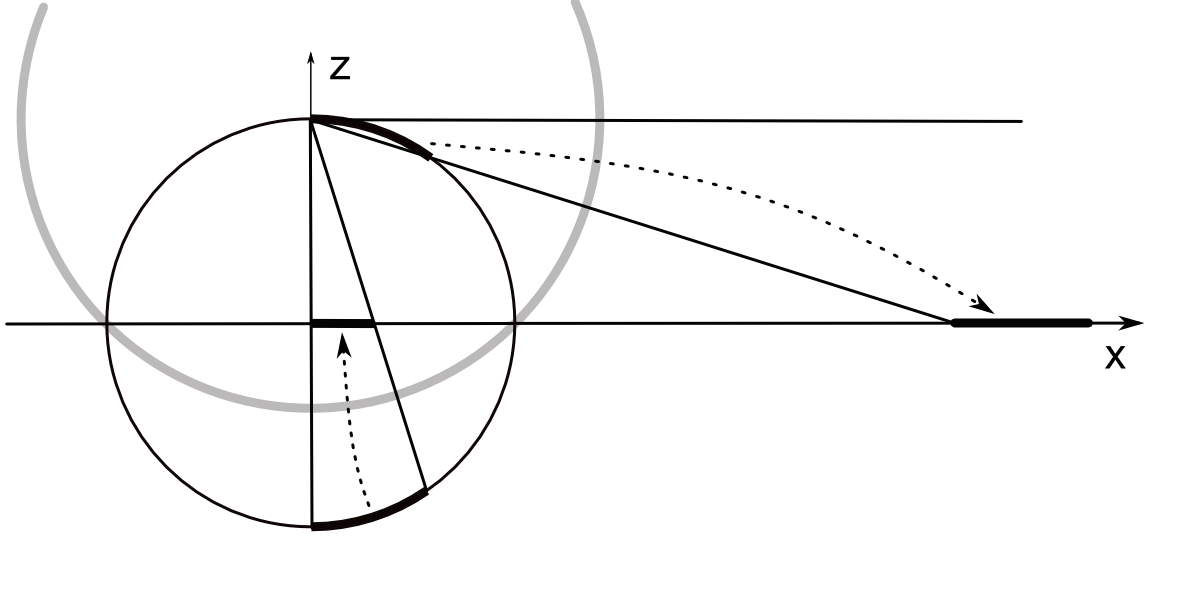
Stereographic projection back into plane.


We have quadrilateral hyperbolic chimney. Hyperbolic reflections in it's sides generate 3-dimensional hyperbolic kaleidoscope.
We look at the pattern created by this kaleidoscope on the surface of Poincare ball mapped to a plane via stereographic projection.


The pattern has two component: inside of a circle is composed of images of the bottom of the chimney.


Outside of the the circle is composed from images of the top of the chimney.


Combined kaleidoscope image.
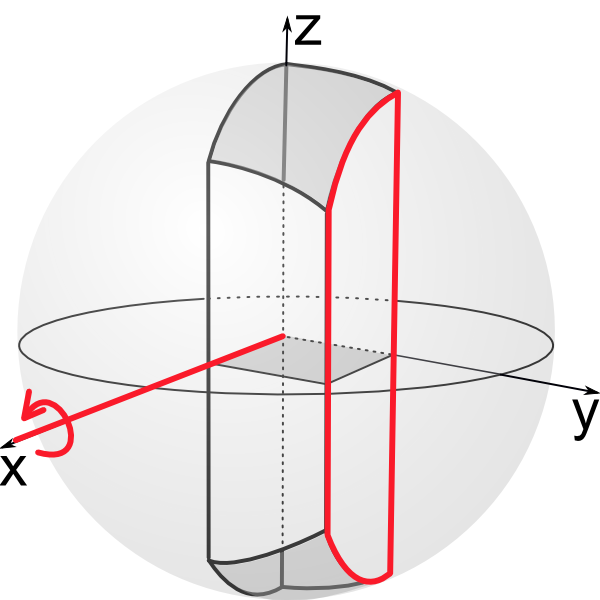
Can we deform *2223 kaleidoscope in 3 dimensions?
We can rotate selected plane about x-axis. This motion will not change dihedral angles of this side of the chimney with it's heighbouring sides.

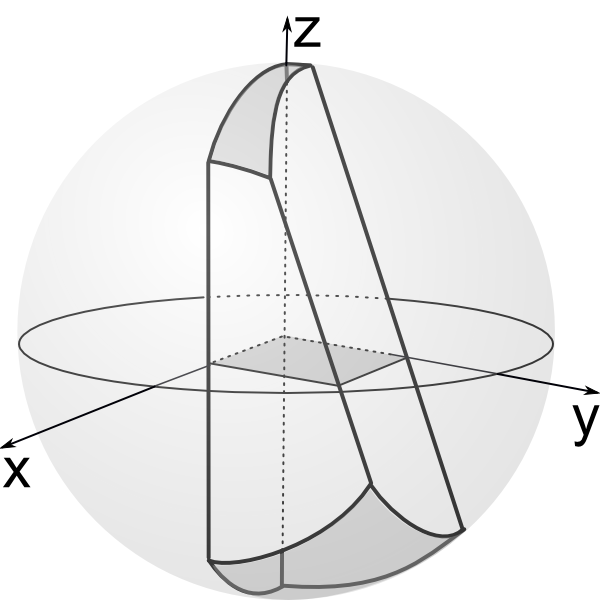

Small tilt.
Disk is transformed into shape with fractal boundary.
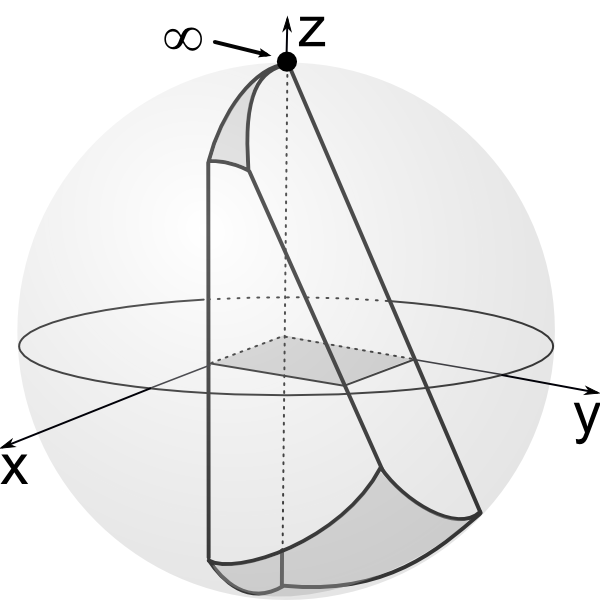

More tilt.
Two sides touch at infinity and make cusp.
Cusp location at `(0,0,1)` causes tiling to expand to infinity.
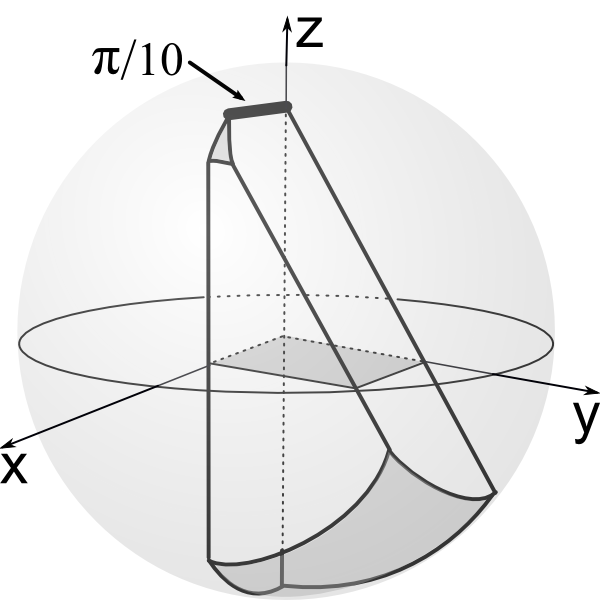

New edge of the "chimney" is partially inside of the unit ball.


Second component of kaleidoscope bursts into fractal set of *2,3,10 triangular kaleidoscopes.


Second component of kaleidoscope bursts into fractal set of *2,3,10 triangular kaleidoscopes.


Second component of kaleidoscope bursts into fractal set of *2,3,10 triangular kaleidoscopes.

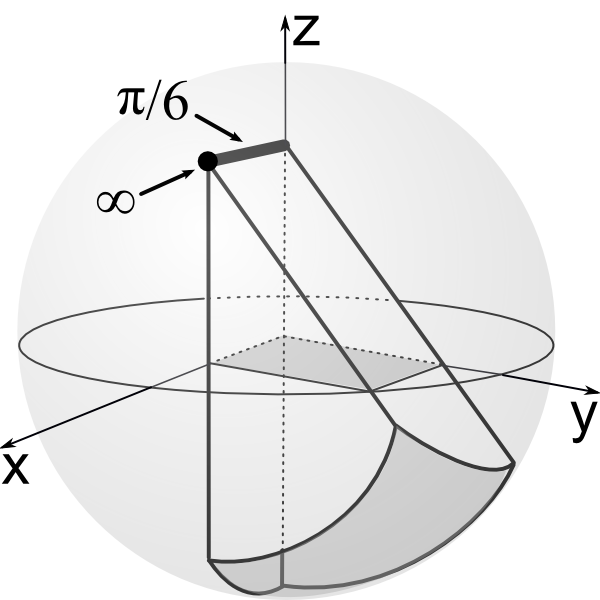
New vertex is formed at infinity. It generates fractal set of euclidean *236 kaleidoscopes.

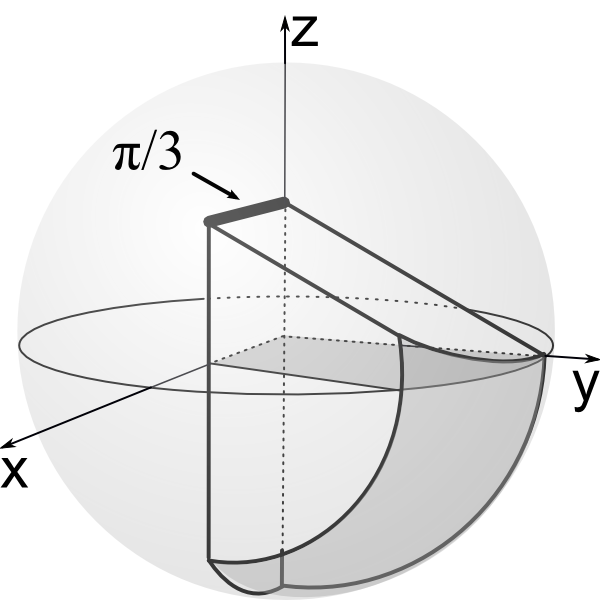
New vertex is moved inside of Poincare ball. Kaleidoscope has now one component.

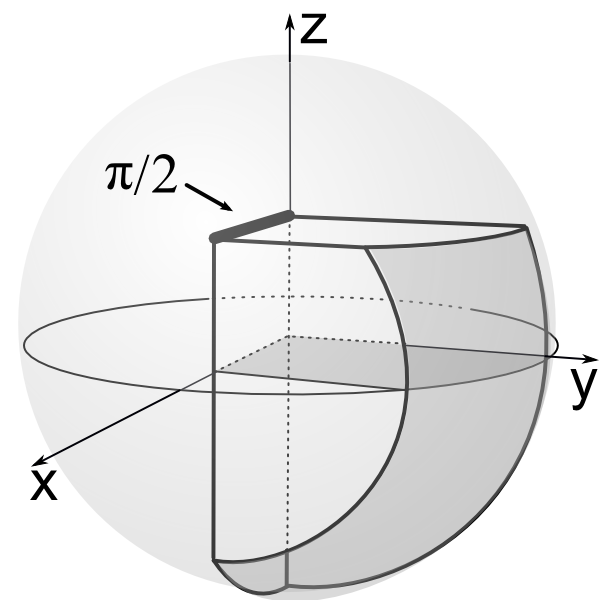
Maximal bend of *2223 kaleidoscope.

Any n-gonal kaleidscope can be bend
n-gonal kaleidoscope has `2(n-3)` independent continuous parameters
`(n-3)` stretching parameters
`(n-3)` bending parameters

Any n-gonal kaleidscope can be bend
n-gonal kaleidoscope has `2(n-3)` independent continuous parameters
`(n-3)` stretching parameters
`(n-3)` bending parameters

Any n-gonal kaleidscope can be bend
n-gonal kaleidoscope has `2(n-3)` independent continuous parameters
`(n-3)` stretching parameters
`(n-3)` bending parameters

Any n-gonal kaleidscope can be bend
n-gonal kaleidoscope has `2(n-3)` independent continuous parameters
`(n-3)` stretching parameters
`(n-3)` bending parameters

Any n-gonal kaleidscope can be bend
n-gonal kaleidoscope has `2(n-3)` independent continuous parameters
`(n-3)` stretching parameters
`(n-3)` bending parameters

Any n-gonal kaleidscope can be bend
n-gonal kaleidoscope has `2(n-3)` independent continuous parameters
`(n-3)` stretching parameters
`(n-3)` bending parameters

Any n-gonal kaleidscope can be bend
n-gonal kaleidoscope has `2(n-3)` independent continuous parameters
`(n-3)` stretching parameters
`(n-3)` bending parameters

Let's play with color.
Tiles from different cosets of a subgroup are colored in different colors.

Let's play with color.
Tiles from different cosets of a subgroup are colored in different colors.

Let's play with color.
Tiles from different cosets of a subgroup are colored in different colors.

Let's play with color.
Tiles from different cosets of a subgroup are colored in different colors.

Let's play with color.
Tiles from different cosets of a subgroup are colored in different colors.

Let's play with color.
Tiles from different cosets of a subgroup are colored in different colors.

Let's play with color.
Tiles from different cosets of a subgroup are colored in different colors.

Let's play with color.
Tiles from different cosets of a subgroup group are colored in different colors.

The last series of images was for bended *2223 kaleidoscope with *236 parabolic subgroup (cusp at infinity).
Similar *2323 kaleidoscope was illustrated before in Klein F., Fricke R. (1897) Vorlesungen Uber die Theorie der Automorphen Functionen

This conformal mapping transforms unit disk to horizontal band
`w =(4/\pi)tanh\^-1(z); z, w \in CC`

This conformal mapping transforms unit disk to horizontal band
`w =(4/\pi)tanh\^-1(z); z, w \in CC`

This conformal mapping transforms unit disk to horizontal band
`w =(4/\pi)tanh\^-1(z); z, w \in CC`

This conformal mapping transforms unit disk to horizontal band
`w =(4/\pi)tanh\^-1(z); z, w \in CC`

This conformal mapping transforms unit disk to horizontal band
`w =(4/\pi)tanh\^-1(z); z, w \in CC`

This conformal mapping transforms unit disk to horizontal band
`w =(4/\pi)tanh\^-1(z); z, w \in CC`

This conformal mapping transforms unit disk to horizontal band
`w =(4/\pi)tanh\^-1(z); z, w \in CC`

This conformal mapping transforms unit disk to horizontal band
`w =(4/\pi)tanh\^-1(z); z, w \in CC`

The mapping works equally well on arbitrary bended kaleidoscope.
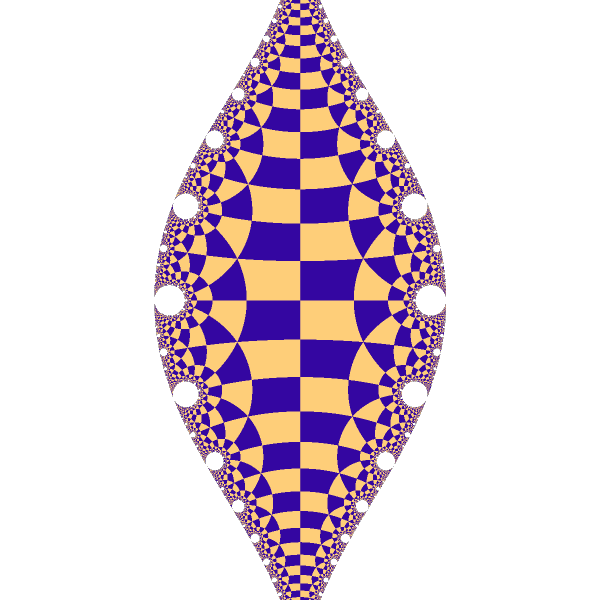
The mapping works equally well on arbitrary bended kaleidoscope.

The mapping works equally well on arbitrary bended kaleidoscope.

The mapping works equally well on arbitrary bended kaleidoscope.

The mapping works equally well on arbitrary bended kaleidoscope.

The mapping works equally well on arbitrary bended kaleidoscope.

The mapping works equally well on arbitrary bended kaleidoscope.

Final step.
We have pattern periodic in x and y-directions.
Pattern can be seamlessly wrapped around cylinder of appropriate radius.

More wild conformally mapped kaleidoscope.

More wild conformally mapped kaleidoscope.

More wild conformally mapped kaleidoscope.

Different coloring of the same kaleidoscope

Different coloring of the same kaleidoscope

Band stretching combined with exponential mappping

Band stretching combined with exponential mappping

Band stretching combined with exponential mappping

What if we bend 4 sided chimney to extreme and make four sided tetrahedron of finite volume?
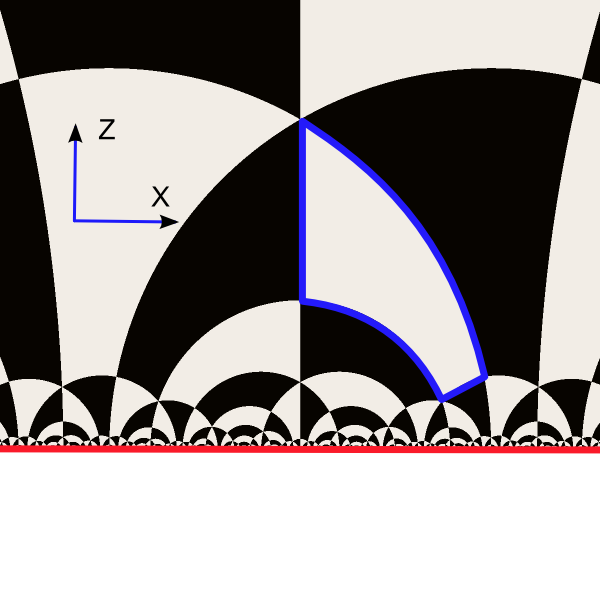
3D tiling with finite fundamental domain
This is XZ plane cross section of the tiling in the upper half space
Tile size tends to zero as we approach the upper half space boundary
Pattern on the boundary of the upper half space disapers

We can take cross section of the 3D tiling through some hyperbolic plane
This will give us something similar to an image of a 2D hyperbolic tiling in the Poincare disk model
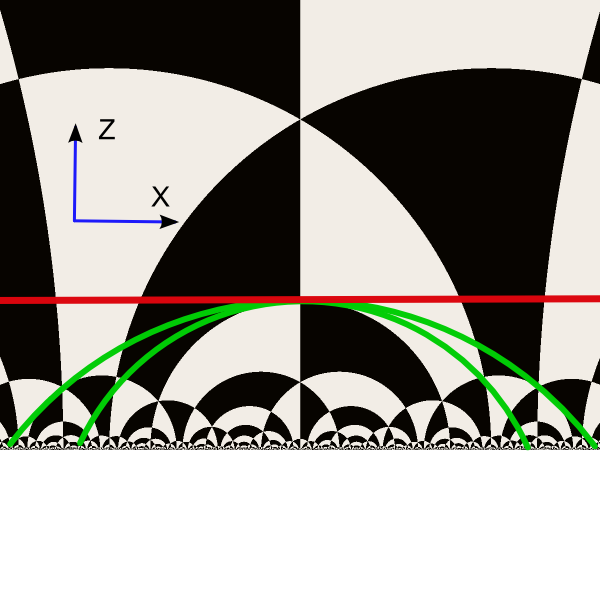
We also can take cross section through series of hypercycles (green) passing via given point. The limit of such hypercycles is horosphere - spherical surface tangent to the boundary of the hyperbolic space.
Here the horosphere (red) touches the boundary at the infinity and it looks like euclidean plane orthogonal to z-axis.

We start with cross section throuth hyperbolic plane. The tiny image of this crossection matched in scale with next series of cross sections through hypercycles and horosphere.

Hypercycle cross section step 1

Hypercycle cross section step 2

Hypercycle cross section step 3

Hypercycle cross section step 4

Hypercycle cross section step 5

Hypercycle cross section step 6

Hypercycle cross section step 7

Hypercycle cross section step 8

Hypercycle cross section step 9

Hypercycle becomes horosphere. All the circles in the pattern are intersections of hyperplanes of the tiling with horosphere.
Hyperbolic metrics inside of horosphere becomes euclidean. Horosphere is in fact a model of the 2D euclidean geometry embedded in 3D hyperblic space.
In contrast to the hyperplane or hypercycle cross sections the pattern in the horosphere cross section has constant scale. The pattern has no periods or repetitions. At the same time pattern looks similar everywhere. This effect is somewhat analogous to some non periodic tilings.

Pattern looks similar everywhere and is different eveywhere.

Pattern looks similar everywhere and is different eveywhere.

Pattern looks similar everywhere and is different eveywhere.

Pattern looks similar everywhere and is different eveywhere.

Combination of horosphere cross section and confomal mapping

This pattern can be seamlessly wrapped around cylinder

More horosphere cross section
_23.png)
More horosphere cross section

More horosphere cross section

More horosphere cross section

More horosphere cross section

Fly through the hyperbolic tiling cutting the tiling with horosphere.
Different colors are used for different cosets of a subgroup of the symmetry group.
youtube animation
Fly through the hyperbolic tiling cutting the tiling with horosphere.
Different colors are used for different cosets of a subgroup of the symmetry group.
youtube animation http://www.youtu.be/35ALc2xUR4Q
Fly through the hyperbolic tiling cutting the tiling with horosphere.
Different colors are used for different cosets of a subgroup of the symmetry group.
youtube animation