

Visual representation of tiling of 3D hyperbolic space attracted very little attention compare to tilings of hyperbolic plane, which were popularized by M.C.Escher circle limit woodcuts. Although there is a lot of activity on theoretical side of the problem starting from work of H.Poincare on Kleinian groups and continuing with breakthrough of W.Thurston in the development of low dimensional topology and G.Perelman's proof of Poincare conjecture.
The book "Indra's Pearl" have popularized visualization of 2D limit set of Kleinian groups, which is located at the infinity of hyperbolic space. In this talk we present our attempts to build and visualize actual 3D tilings. We study tilings with symmetry group generated by reflections in the faces of Coxeter polyhedron, which also is the fundamental polyhedron of the group.
Online address of the talk:
bulatov.org/math/1101/
These are some of the people involved in the development of the hyperbolic geometry and
classification of symmetry groups of hyperbolic plane and space:
N.Lobachevski, Janos Bolyai, F.Klein, H.Poincare, D.Coxeter, J.Milnor, J.Hubbard, W.Thurston, B.Mandelbrot, G.Perelman










.jpg)
|
The first high quality drawing of 2D hyperbolic tiling apperas 1890 in book by Felix Klein and Robert Fricke. This is drawing of *237 tessellation from F.Klein and R.Fricke "Vorlesungen über die Theorie der Elliptischen Modulfunctionen," Vol. 1, Leipzig(1890) |
|
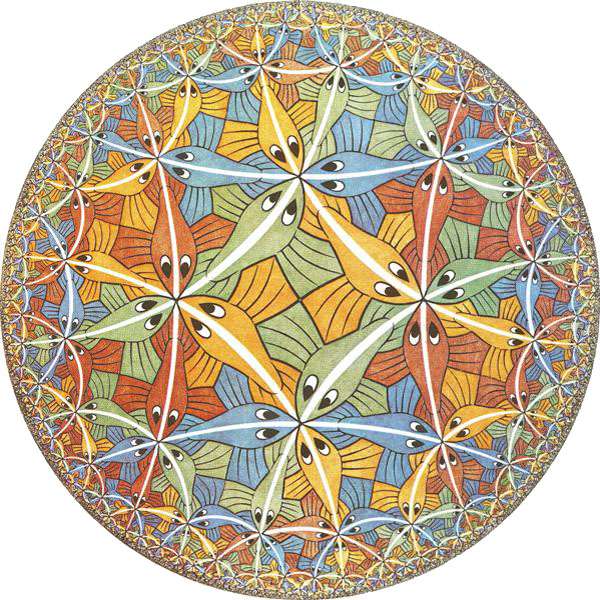
M.C.Escher Circle Limit III (1958) He was inspired by drawing of hyperbolic tiling in paper of H.S.M.Coxeter. |

|
Many hyperbolic patterns by D.Dunham |

|
C.Goodman-Strauss's graphics work. |
|
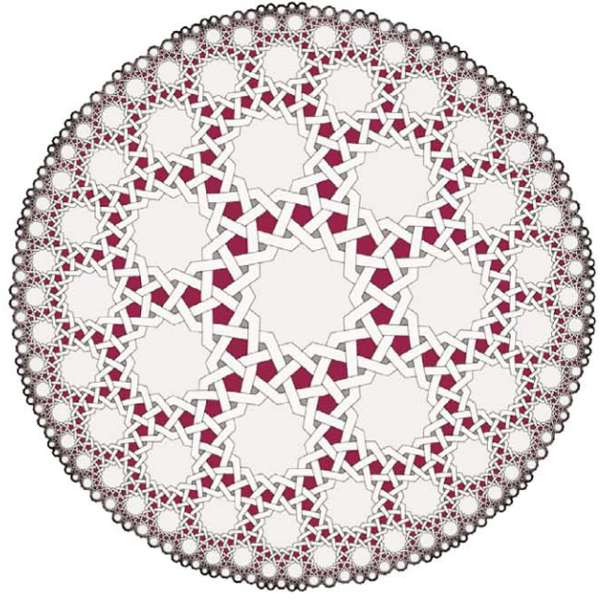
C.Kaplan's Islamic pattern. |

|
Martin von Gagern "Hyperbolization of Euclidean Ornaments" |
|
3D tilings were visualized by rendering it's 2D limit set on the infinity of the hyperbolic space.
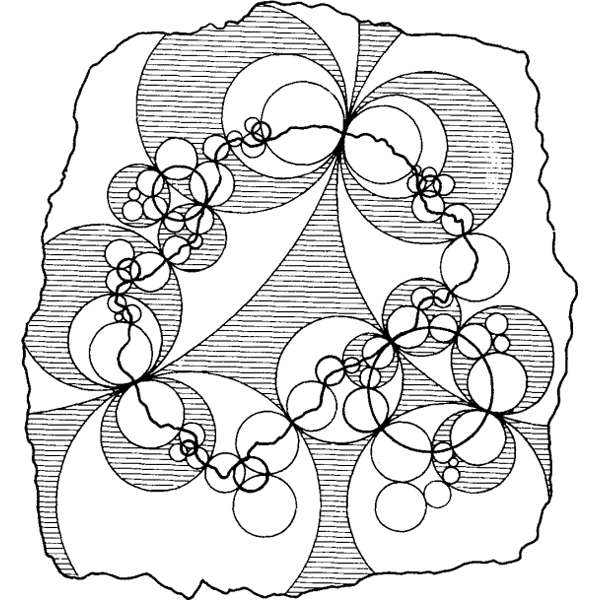
One of the first know drawings of limit set from F.Klein and R.Fricke "Vorlesungen über die Theorie der Automorphen Functionen" Leipzig(1897) This hand drafted image was the best available to mathematicians until 1970s, when B.Mandelbrot started to make computer renderings of Kleinian groups |

|
B.Mandelbrot's computer rendering of Kleinian group (from Un ensemble-limite par Michele Audin et Arnaud Cheritat (2009)) |

|
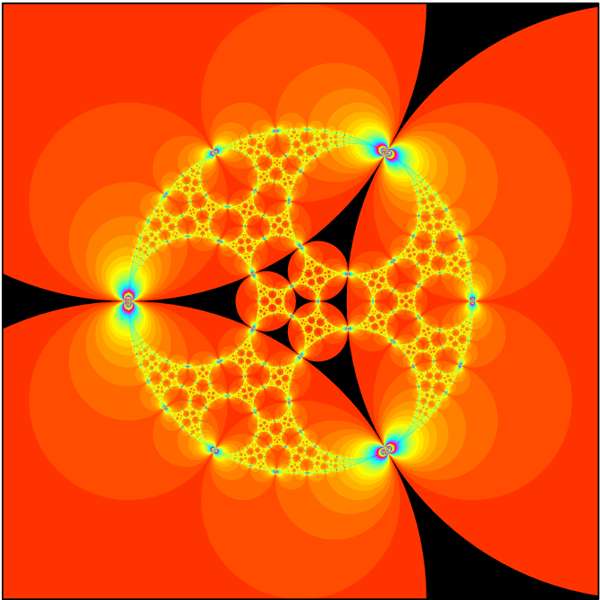
Interactive applet of the kleinian group visualization by Arnaud Cheritat. From Un ensemble-limite. |
|
"Indra Pearl" by D.Mumford, C.Series and D.Wright (2004) popularized visualization of limit sets of Kleinian groups. |

|
Kleinian group images by Jos Leys. His very artistic images rendered as 3D images represent essentially 2-dimensional limit set of Kleinian group. |
|
Coxeter polygon: All angles are submultiples of `pi`:
`alpha_i = pi/m_i`. Here all four angles of euclidean polygon are equal `pi/2` |
|
The tiling is generated by reflections in the sides of the Coxeter polygon. Here we have original tile and second generation of tiles. |
|
First, second and third generation of tiles. Condition on angles `alpha_i = pi/m_i` guaranties, that tiles fit without gaps. `2 m_i` tiles meet at each vertex. |
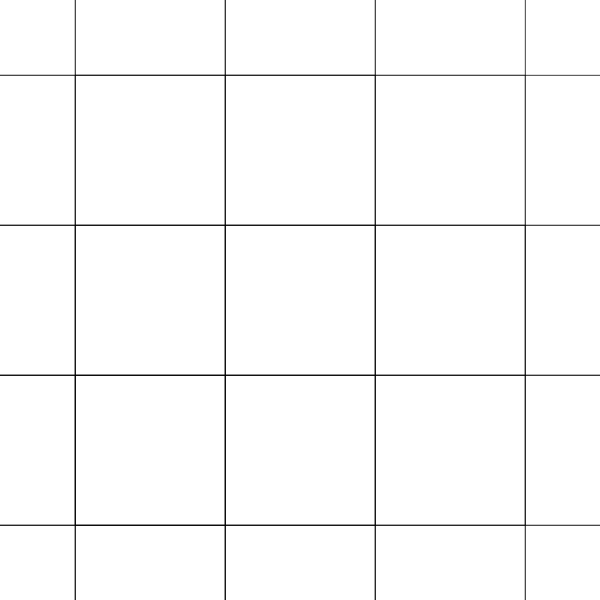
|
Complete tiling - regular rectangular grid. |
|
Hyperbolic Coxeter pentagon with all `alpha_i = pi/2` shown in the Poincare disk model of hyperbolic plane. The shape of the right angled pentagon has 2 independent parameters (two arbitrary sides lengths). Lengths of any two sides can be chosen independently. The length of three remaining sides can be found from hyperbolic trigonometry identities. |
|
Base tile is hyperbolically reflected in the sides of the Coxeter polygon. |
|
First, second and third generations of tiles. |
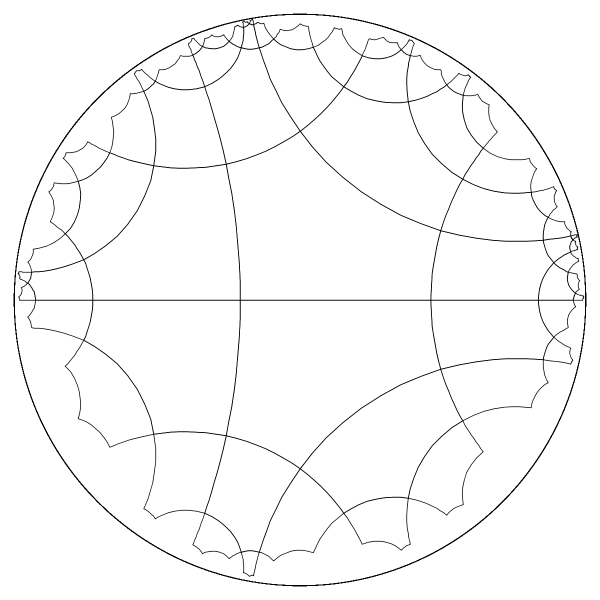
|
Four generations of tiles. |
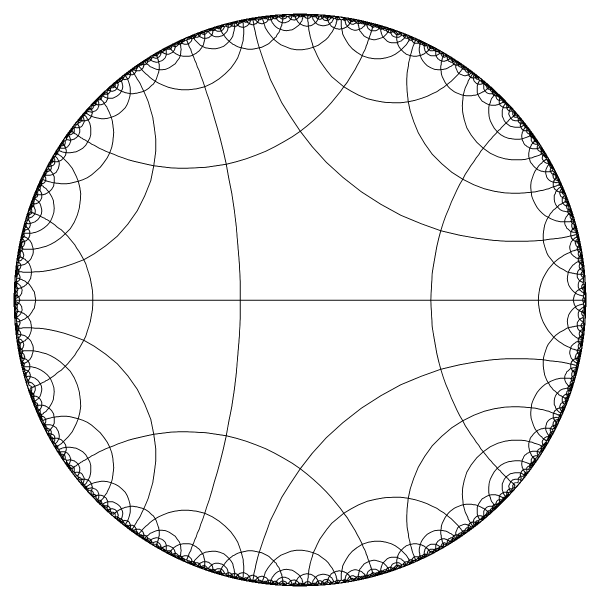
|
Complete tiling in the Poincare disc model of hyperbolic plane. |
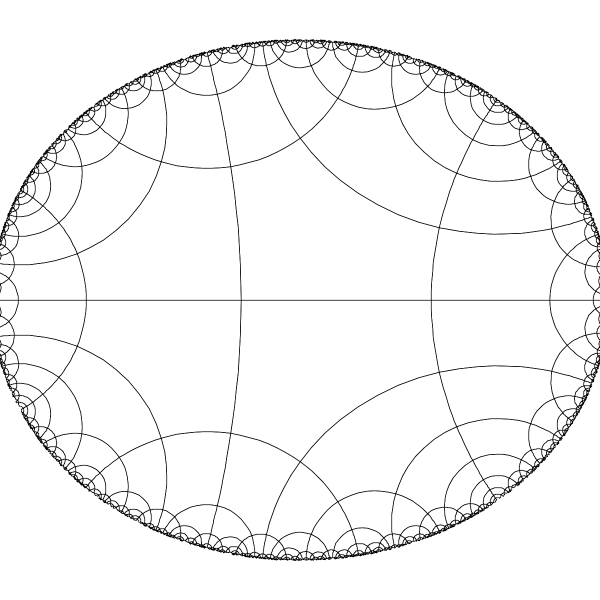
|
To make another view of the same tiling we can conformally stretch the Poincare disk into an infinite band. |
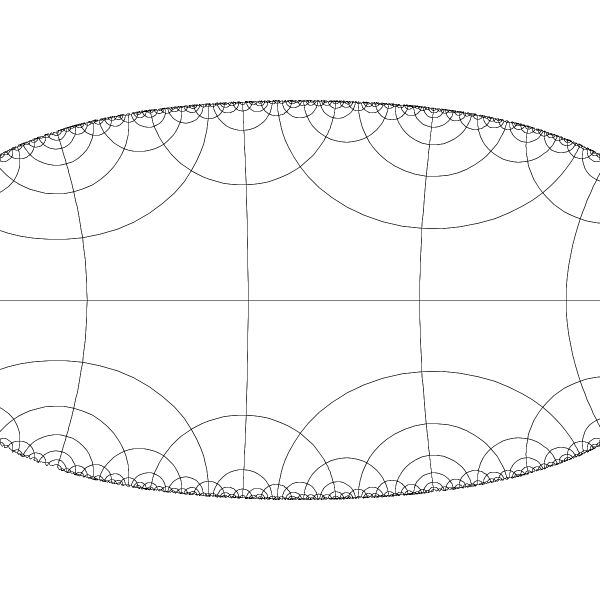
|
To make another view of the same tiling we can conformally stretch the Poincare disk into an infinite band. |
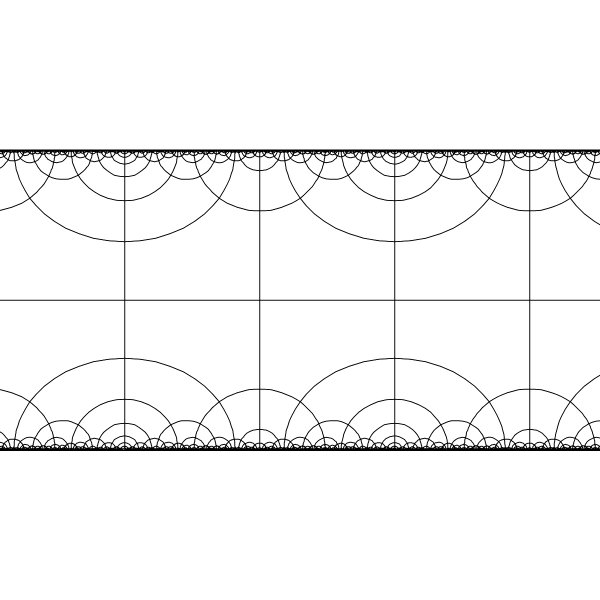
|
Tiling in the band model of the hyperbolic plane. The hyperbolic metric along horizontal axis of the band is euclidean. As a result the tiling has euclidean translation symmetry in horizontal direction. The tiling has translation symmetry along each of the geodesics shown, but only horizontal translation is obvious to our euclidean eyes. |
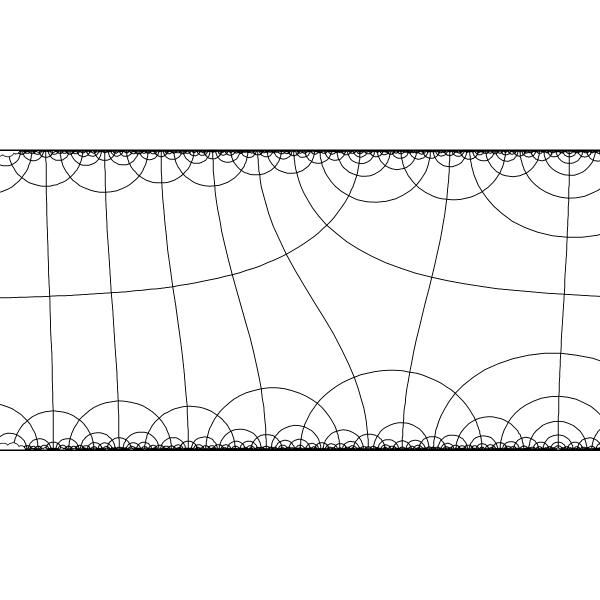
|
Appropriate hyperbolic isometry can send any 2 selected points to `+- oo` of the band model. |
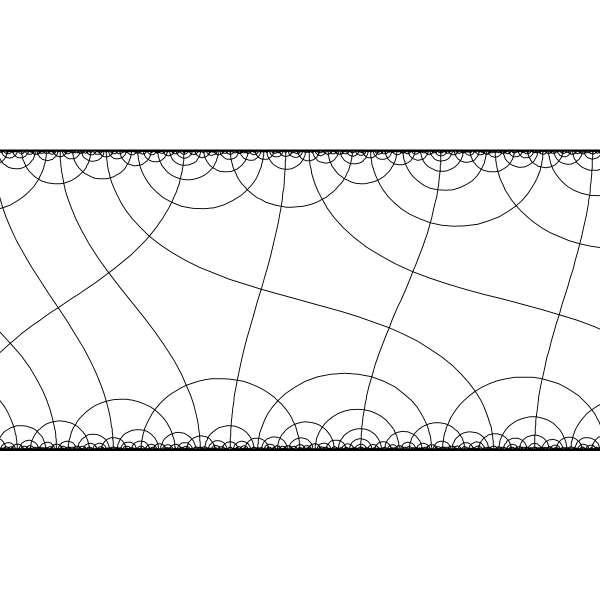
|
Appropriate hyperbolic isometry can send any 2 selected points to `+- oo` of the band model. |
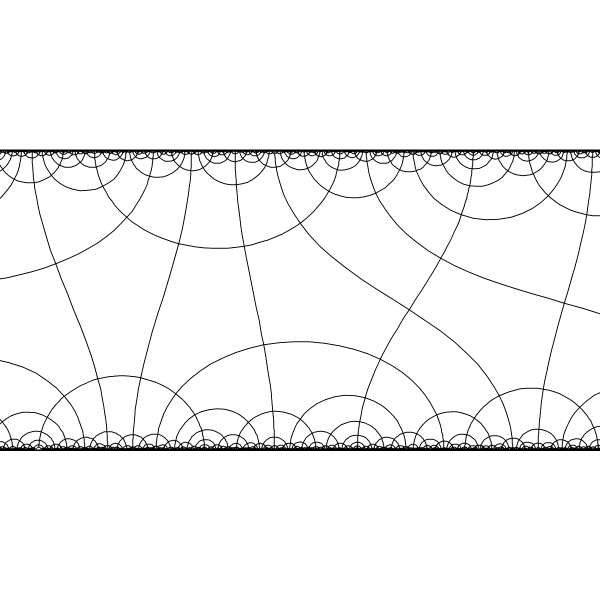
|
Appropriate hyperbolic isometry can send any 2 selected points to `+- oo` of the band model. |
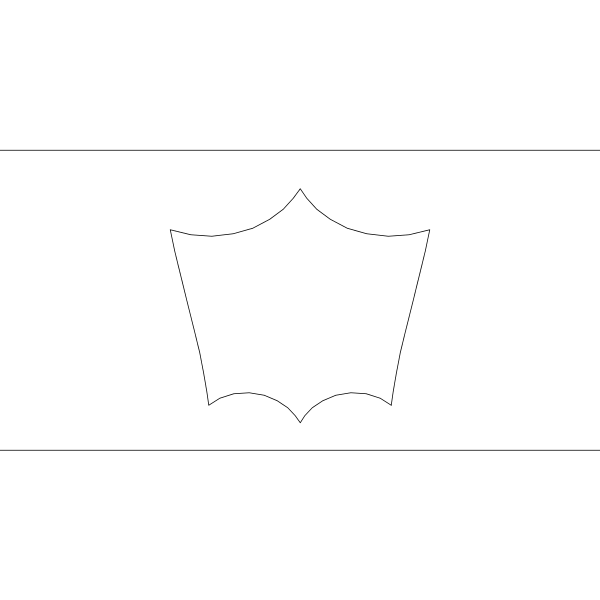
|
Hyperbolic Coxeter N-gon exist for any `N >=5` and angles `alpha_i = pi/m_i m_i >= 2` The space of shapes of Coxeter N-gon has dimension `N-3`. |
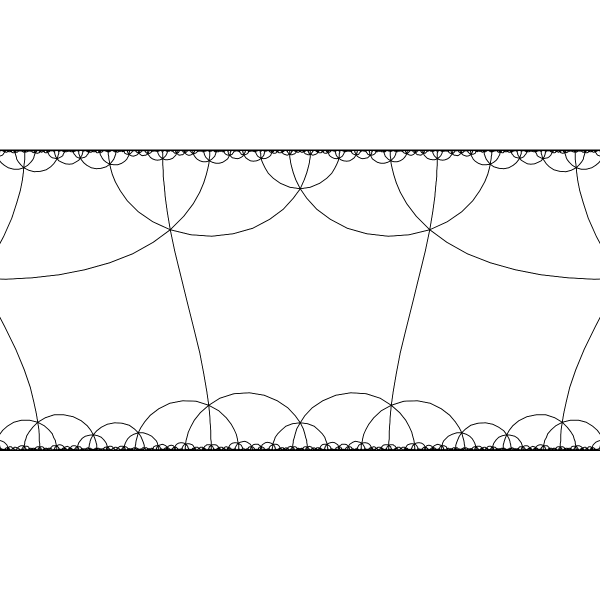
|
Example. Tiling of hyperbolic plane with Coxeter hexagons with all angles equal `pi/3`. |
|
Dihedral angles of Coxeter polyhedron are submultiples of `pi`: `delta_i = pi/m_i`.
Reflections in sides of Coxeter polyhedron satisfy conditions of Poincare Polyhedron Theorem. Therefore the reflected copies of such polyhedron fill the space without gaps and overlaps. Example - euclidean rectangular parallelepiped. |
|
First and second generation of tiling of the euclidean space by rectangular parallelepipeds. We can easy imagine the rest of the tiling - infinite regular grid. |
|
Coxeter polyhedra in hyperbolic space Do they exist? |
|
From Andreev's Theorem(1967) on compact polyhedra with non-optuse dihedral angles in hyperbolic space follows:
There exist unique compact Coxeter polyhedron in hyperbolic space iff: |
|
Example of polyhedron satisfying Andreev's theorem. The polyhedron is combinatorially equivalent to a cube with one truncated vertex. |

|
Visualization of the actual geometric realization of truncated cube in the hyperbolic space shown in the Poincare ball model. |

|
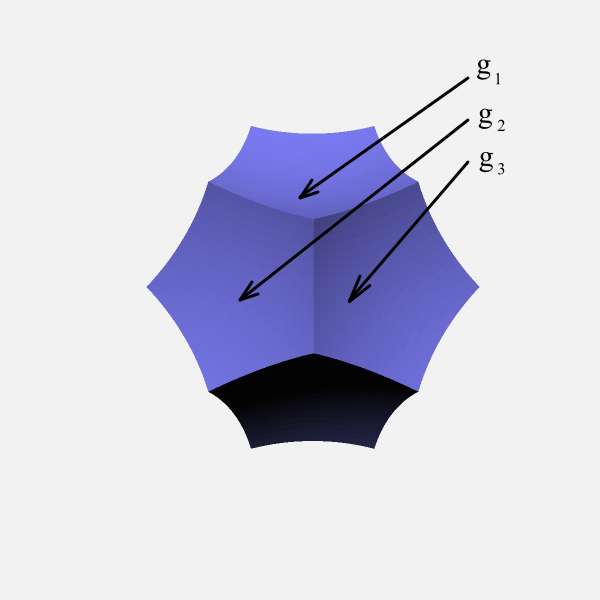
Regular right angled hyperbolic dodecahedron All dihedral angles are equal `pi/2` All faces are regular right angled hyperbolic pentagons |
|
From Andreev's Theorem(1967) on polyhedra of finite volume with non-optuse dihedral angles in hyperbolic space follows:
There exist unique Coxeter polyhedron in `H^3` if |

|
Tetrahedron with all dihedral angles `pi/3`. All 4 vertices are ideal. |

|
Octahedron with all dihedral angles `pi/2`. All 6 vertices are ideal. |
|
Coxeter polyhedra in Euclidean space |
Coxeter polyhedra in Hyperbolic space |
|
Only 7 non-equivalent types of compact polyhedra:
|
|
|
Coxeter polyhedra in Euclidean space |
Coxeter polyhedra in Hyperbolic space |
|
|
|
|
|
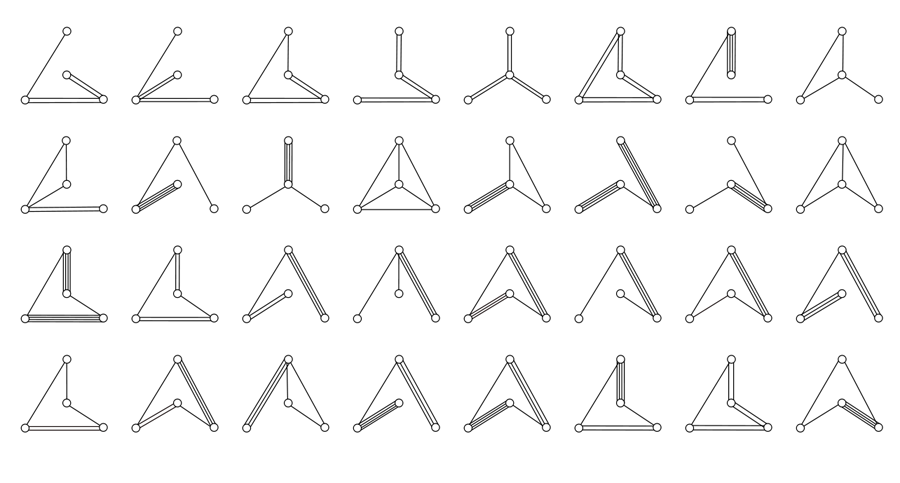
|
"Hand" calculation for simpler polyhedra:
General method: Roeder R. (2007) Constructing Hyperbolic Polyhedra Using Newton's Method. |

|
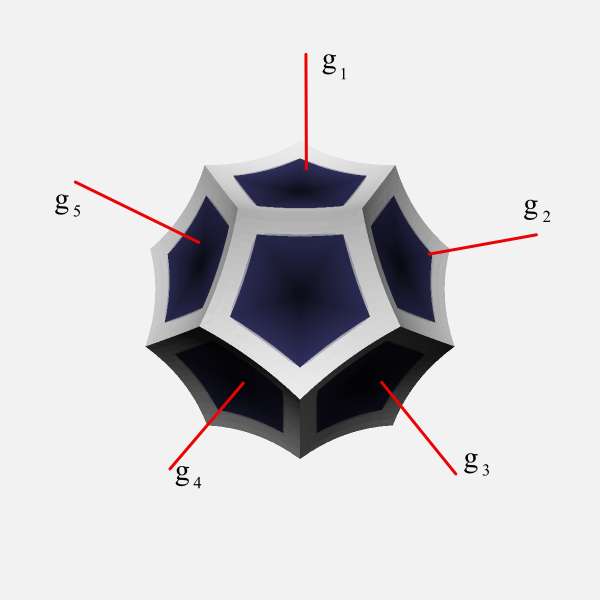
Regular right angled dodecahedron. 12 generators of the tiling are reflections in each of 12 dodecahedron's faces. |

|
Regular right angled dodecahedron. |
|
Regular right angled dodecahedron. |

|
Regular right angled dodecahedron. |

|
Regular right angled dodecahedron. |

|
Regular right angled dodecahedron. |

|
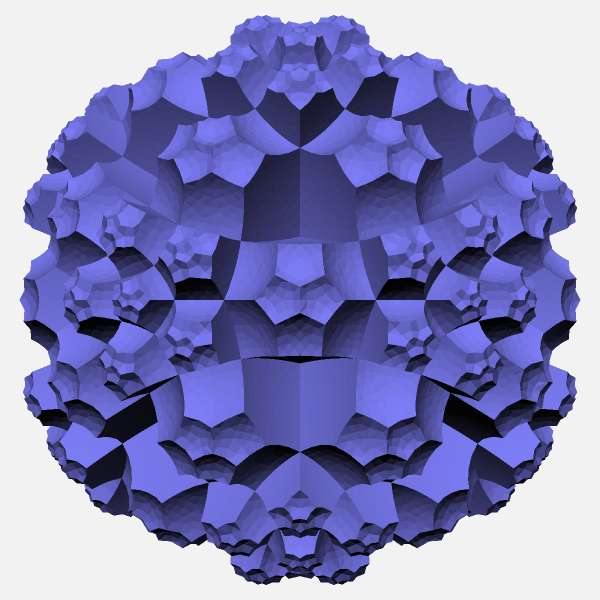
Just kidding! It is a sphere, which is good approximation to `10^10` dodecahedral tiles. |

|
Different approach - rendering only edges |

|
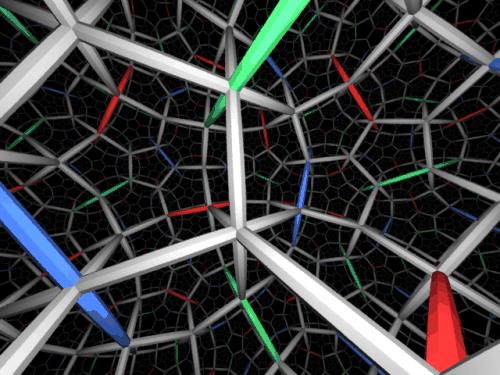
Another approach - looking at the tiling from inside of the space (W. Thurston, J. Weeks). This allows to see clearly the local structure of the tiling. Image by Tom Ruen from wikipedia.org generated by Jeff Weeks interactive software. Similar image from "Knot plot" video was used on cover of dozens of math books. |
|
Hyperbolic space tessellation as it looks from inside the space. Frame from "Not Knot" video (1994)
|
|
Looking from inside we can see only nearest neighbours. Looking from outside we can only see the outer boundary. Let's try to look outside, but see not the whole tiling, but only it's part. We select only subset of all generators. The subset will generate subgroup of the whole group. |

|
First iteration of subgroup generation. |

|
Second iteration of subgroup generation. |

|
Third (and last) iteration of subgroup generation. |

|
Move center of the shape into the center of the Poincare ball. Shape has obvious cubic symmetry. |

|
Another view of the same finite subtiling. We have 8 dodecahedra around center |
|
We can select generators, which generate infinite subgroup. |

|
First iteration. |

|
Second iteration. |

|
Third iteration. |

|
Few more iterations. All tiles are lying in one hyperbolic plane. |

|
Rotation of the tiling around the center of the ball. |

|
Rotation of the tiling around the center of the ball. |

|
Rotation of the tiling around the center of the ball. |

|
Rotation of the tiling around the center of the ball. |

|
Hyperbolic translation of plane into the center of the ball. |

|
Hyperbolic translation of plane into the center of the ball. |

|
More rotation about the center of the ball. |

|
More rotation about the center of the ball. |

|
More rotation about the center of the ball. |

|
More rotation about the center of the ball. |

|
More rotation about the center of the ball. |

|
Stretching the Poincare ball into infinite cylinder. |

|
Stretching the Poincare ball into infinite cylinder. |

|
Stretching the Poincare ball into infinite cylinder. |

|
Stretching the Poincare ball into infinite cylinder. |

|
Stretching the Poincare ball into infinite cylinder. |

|
Stretching the Poincare ball into infinite cylinder. |

|
Cylinder model is straighforward axially symmetric 3D generalization of the conformal band model of the hyperbolic plane. Cylinder model of hyperbolic space is not conformal, it has some limited angular distorsions. However, it has such a nice property as euclidean metrics along cylinder's axis. It is especially usefull when we want to visualize some specific hyperbolic geodesic which we aling in that case with the cylinder's axis. All the planes orthoginal to that geodesic are represented by circular disks orthogonal to the axis. |

|
If cylinder's axis is aligned with the axis of a hyperbolic transformation of the group, tiling will have euclidean translational symmetry along the cylinder's axis. If it is aligned with the axis of a loxodromic transformation, tiling will spiral around the cylinder's axis. Different orientation of the same tiling inside of cylinder model of hyperbolic space. |

|
Different orientation of the same tiling inside of cylinder model of hyperbolic space. This group has no loxodromic transformatons. |

|
Different orientation of the same tiling inside of cylinder model of hyperbolic space. Transformation with longer period is aligned with the cylinder's axis. |

|
Different orientation of the same tiling inside of cylinder model of hyperbolic space. No period is visible. |

|
Different subset of generators generates tiling, which is not flat anymore. |

|
Another orientation of the same tiling. |

|
Another orientation of the same tiling. |

|
Another orientation of the same tiling. |

|
Axis of cylinder is aligned with the axis of a loxodromic transform. |

|
Axis of cylinder is aligned with the axis of different loxodromic transform. |

|
Quasifuchsian tiling with Lambert cubes show in the Poincare ball model. Only 4 out of 6 generators are used. |

|
Quasifuchsian tiling with 5 and 9 sided prisms. |

|
Quasifuchsian tiling with 5 and 18 sided prisms. |

|
Tiling with right angled dodecahedra. Limit set is point set. |

|
Tiling with rhombic triacontahedra in the cylinder model. |

|
Tiling with rhombic triacontahedra. |

|
Tiling with truncated tetrahedra. Axis of cylinder model is vertical and it is aligned with common perpendicular to two selected planes. These planes become flat in the cylinder model and are at the top and bottom of the piece. |
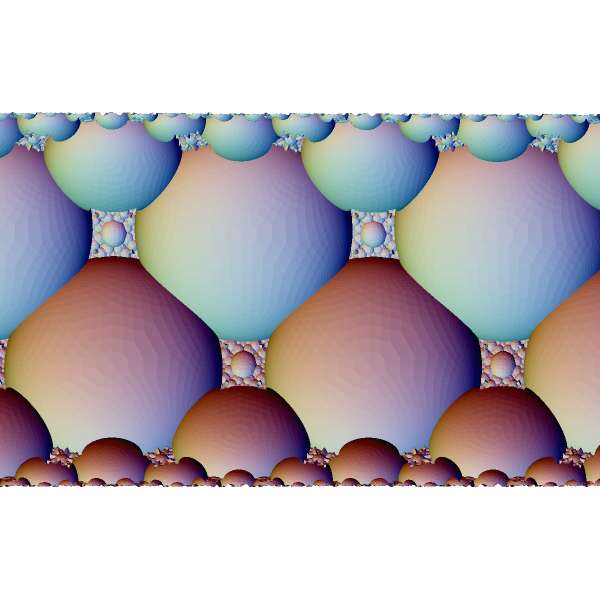
|
Tiling with different truncated tetrahedra in cylinder model. Axis of cylinder is aligned with axis of some hyperbolic transformation of the group, which makes tiling periodic. |
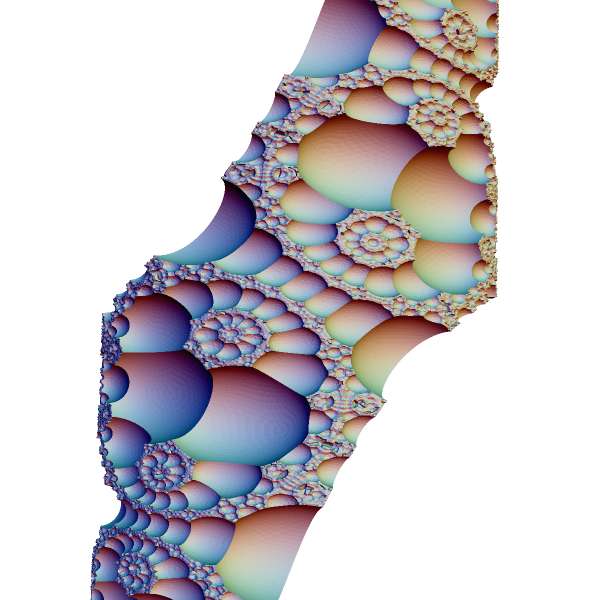
|
Tiling with truncated Lambert cubes. The limit set is complex fractal. |

|
Another tiling with truncated cubes. |

|
Tiling with two generator free group. Shown in the cylinder model. Generators have parabollic commutator, which is responsible for cusps. |

|
The same tiling in shown in the Poincare ball model. |

|
The same tiling in shown in the cylinder model. Axis of cylinder is aligned with axis of some hyperbolic transformation. It makes tiling periodic. |

|
Tiling with two generator free group shown in the cylinder model. Generators have almost parabolic commutator. |
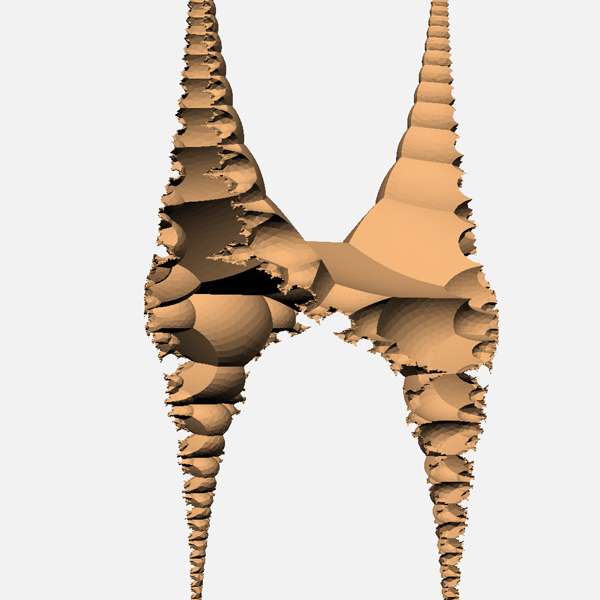
|
Tiling with group with parabolic commutator shown in the cylinder model. Fixed points of two parabolic transformations are located at the cylinder's axis at infinity. |

|
Some quasifuchsian group with 5 generators shown in the cylinder model. |
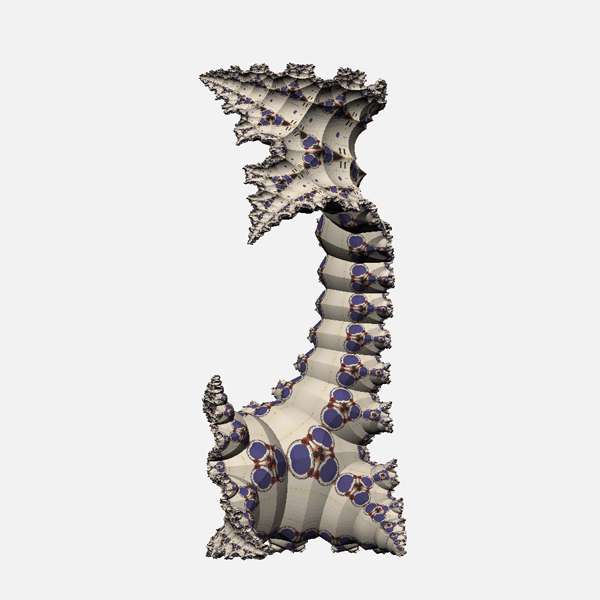
|
Wild quasifuchsian group. |

|
Wilder quasifuchsian group. |

|
Tiling with truncated cubes in the cylinder model. Placing repeating pattern on the surface reveals the *455 tiling structure on the hyperplanes, which corresponds to `pi/4`,`pi/5`,`pi/5` triangle formed at the truncated vertex. |

|
Another orientation the same tiling with cubes in the cylinder model. The axis of cylinder model is perpendicular to one selected plane, which make this plane at the bottom flat. |

|
Another orientation the same tiling. *455 pattern is repeated at every exposed plane. |

|
Another orientation the same tiling. To find this orientation we selected a loxodromic transformation with small rotational and large translational components. Next we selected 2 hyperbolic planes with poles near the 2 fixed points of the transformation and have alligned common perpendicular to these planes with the axis of the cylinder model. |

|
Another orientation of the same tiling. One plane at the bottom is perpendicular to the cylinder axis. Another plane is almost parallel the the axis, making long tong at the top. |

|
Another orientation of the same tiling with cubes in the cylinder model. One of the hyperplanes is very close to the cylinder's axis and is stretched almost to the vertical band. On the top and at the bottom of the tiling there are flat hyperplanes, which have their common perpendicular aligned with the cylinder's axis. |

|
Tiling at the boundary of hyperbolic space shown in stereographic projection to 2D. |

|
Tiling at the boundary of hyperbolic space shown in stereographic projection to 2D. |

|
Tiling at the boundary of hyperbolic space shown in stereographic projection to 2D. |

|
Tiling at the boundary of hyperbolic space shown in stereographic projection to 2D. |

|
Tiling at the boundary of hyperbolic space shown in stereographic projection to 2D. |

|
Metal sculpture. 20 Dodecahedra. |

|
Metal sculpture. First iteration of Weber-Seifert dodecahedral tiling. |

|
Metal sculpture. 20 hyperbolic cubes. |

|
Metal sculpture. Tiling by Fuchsian group. |

|
Hyperbolic bracelet. |

|
Hyperbolic bracelet. |

|
Hyperbolic bracelet. |

|
Hyperbolic bracelet. |

|
Hyperbolic pendant. |

|
Hyperbolic pendant. |

|
Hyperbolic pendant. |

|
Hyperbolic sculpture. |

|
Hyperbolic sculpture. |

|
Hyperbolic sculpture. |

|
Online address of the talk: |